Probability distributions and random variables
Psychology and Child Development
Previous class
In our last session we talked about DATA (uppercase) and data (lowercase).
We studied that DATA means all the possible values in Nature for instance, all the college students in US versus a single fix observation called data (lowercase)
In this session is important to remember this convention.
DATA means random variable whereas data means fixed quantities.
For instance, in a dice you have 6 possible values, when roll a dice ; let’s imagine you get 5 , then your data is y = 5 while you DATA is any possible value from 1 to 6.
Random variables have a distribution, this means DATA is random.
Types of DATA
Nominal DATA: These are DATA whose possible values are essentially labels (or, as the word nominal suggests, names), with no numerical value. Ex: marital status, job title, political affiliation.
Continuous DATA: These are numerical DATA whose possible values lie in a continuum, or in a continuous range. For instance the duration of this class in seconds.
Ordinal DATA: These types of DATA are intermediate between nominal and continuous. Unlike nominal data, which can be numbers without intrinsic order such as 1 = male and 2 = female, ordinal DATA are numbers that reflect an intrinsic order, hence, the name ordinal. Example, education level, ranking of your favorite dessert.
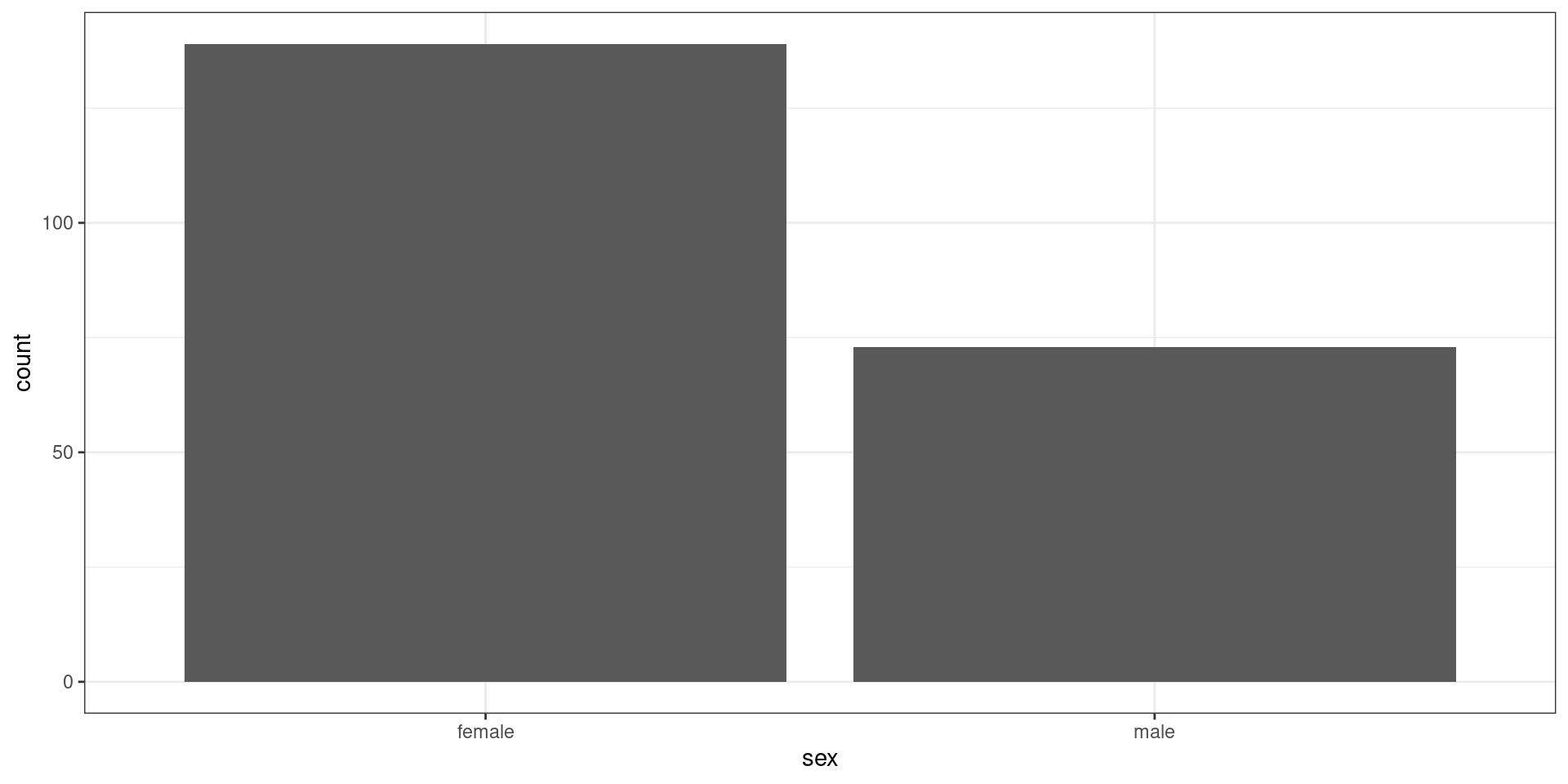
Nominal data
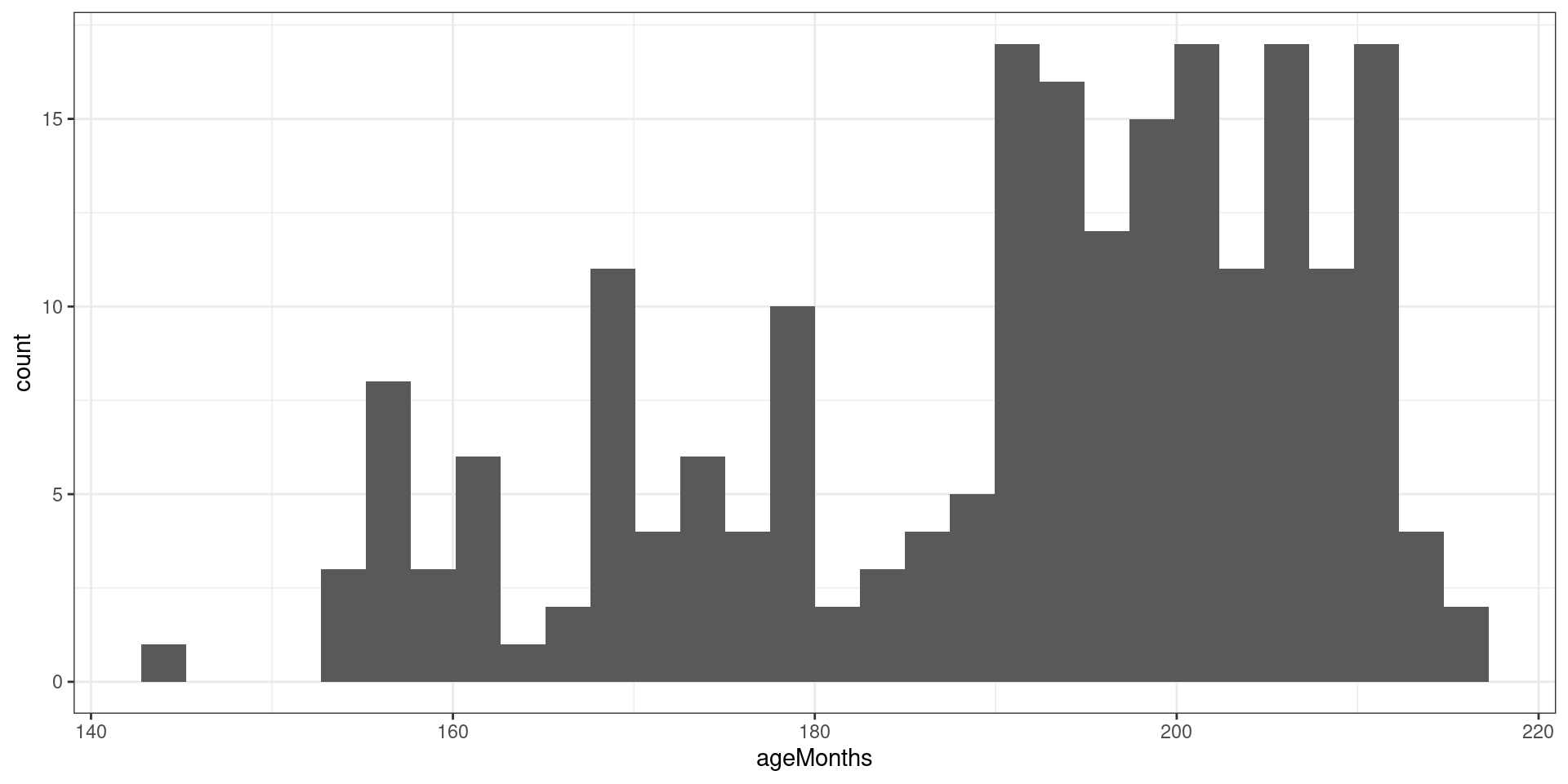
Continuous data
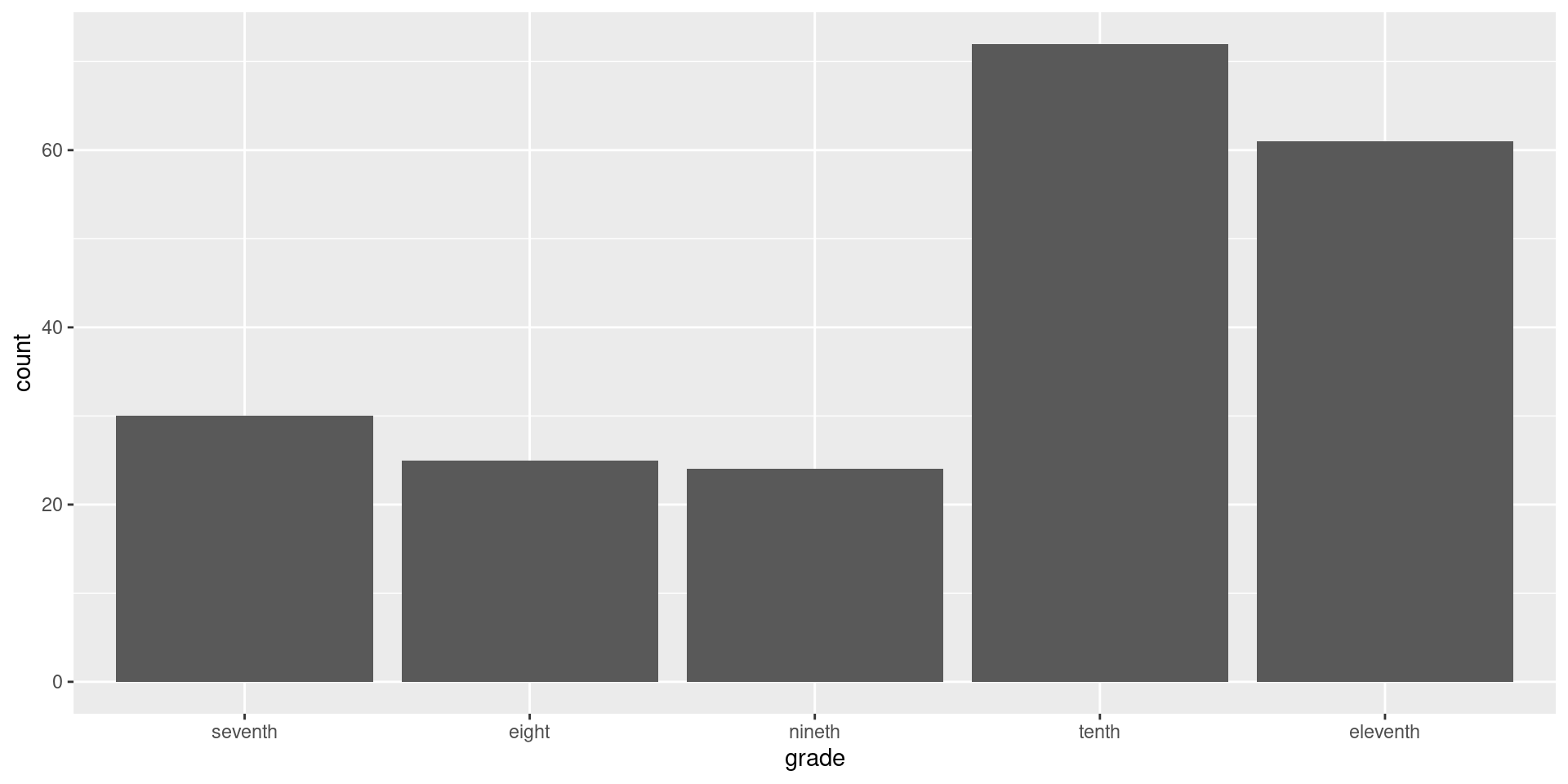
Ordinal data
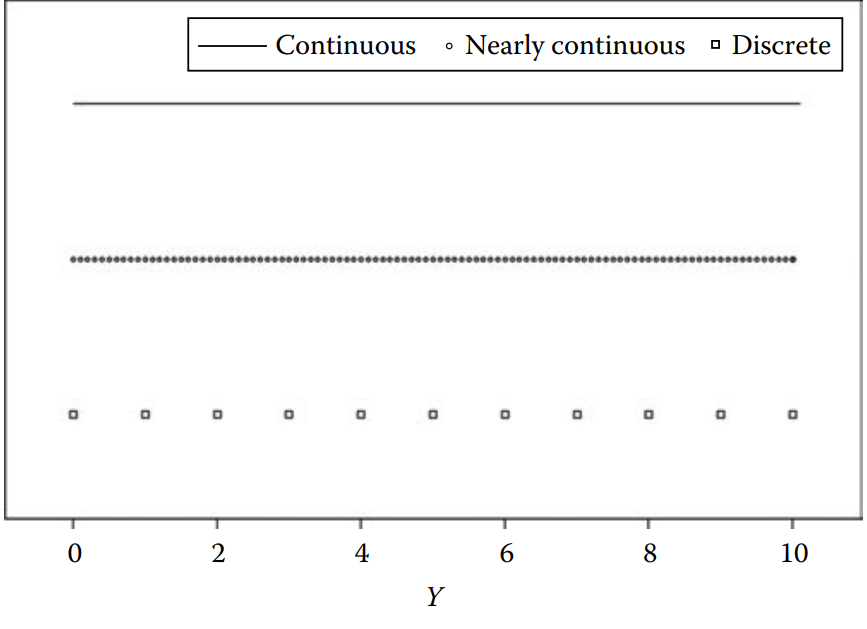
Discrete vs. Continuous
Nominal and Ordinal DATA are considered discrete DATA, this means that values can be listed.
Continuous DATA cannot be listed because all possible values lie in a continuum.
Discrete Probability Distribution Functions
- In our previous class I mentioned the concept of probability density function (pdf), in simple words, the pdf is the model for a random variable.
- For example, you can assume that the pdf of the normal distribution produces you DATA. DATA such as grades in all the statistics classes in US can be assumed to be generated by a normal distributed model.
- We will revisit more about the normal distribution in this class.
Discrete Probability Distribution Functions
But let’s focus on discrete distributions first.
As I said before, a discrete variable can be listed as showed below:
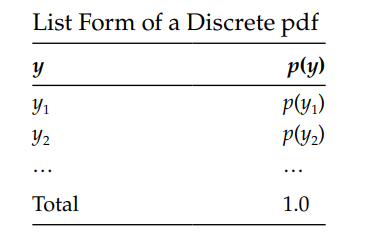
- In this table \(p(y)\) represents the probability of any variable \(y\).
- When we talk about discrete distributions we talk about probability mass function , when the variable is continuous we used the concept probability density function.
Discrete Probability Distribution Functions II
A Discrete pdf or probability mass function has several requirements:
- The probabilities are NEVER negative, but they could be zero.
- The total probability is 1.0 or 100%
Discrete Probability Distribution Functions III
Probability distributions are the most important component in statistics.
We always talk about the normal distribution model, however there several different distributions in the universe. But we are going to study only a few of them.
Do you remember the coin example? The right model for the coin problem is the pdf discovered by Bernoulli. In fact, many people call it the Bernoulli distribution. Its formal representation is as follows:
- No worries about the interpretation of the formula, we might have time to study this distribution at the end of this course. Let’s focus on how we can use this model.
Simulation time!
Remember the mantra: Models produce data, this means we can produce data using the Bernoulli model:
Let’s think about the tossing the coin, we can assign numerical values to the the results, for instance each time we get a head we will code it as 1.00, when we get tail we’ll code it as 0.00.
In the
Rcode above, I’m simulating tossing a coin randomly 100 times using the discrete Bernoulli distribution, after doing that I get exactly zeros and ones, as we expected. Now, following the coin toss model, we should have a probability \(p(heads)= 0.50\) in the long run.But wait? Why we don’t get 0.50? According to our simulated data we have a probability of 0.48.
Let’s try again but this time lets generate 1006 values:
- That’s magic! Now we have 0.50 probability of getting heads, what happened?
- When we have more observed data we are closer to the DATA generating process value. The value for our unknown parameter is 0.50 according to our model, after adding more data, we are close to that number. This is also called the Law of Large Numbers.
We don’t simulate fliping coins all the time…
Bartoš et al. (2023) tested several questions associated to flipping coins.
Several participants flipped coins up to a total of 350,757 flips.
Let’s play with their data.
How many times will the coin land on the same side as where it started?

We don’t simulate fliping coins all the time…
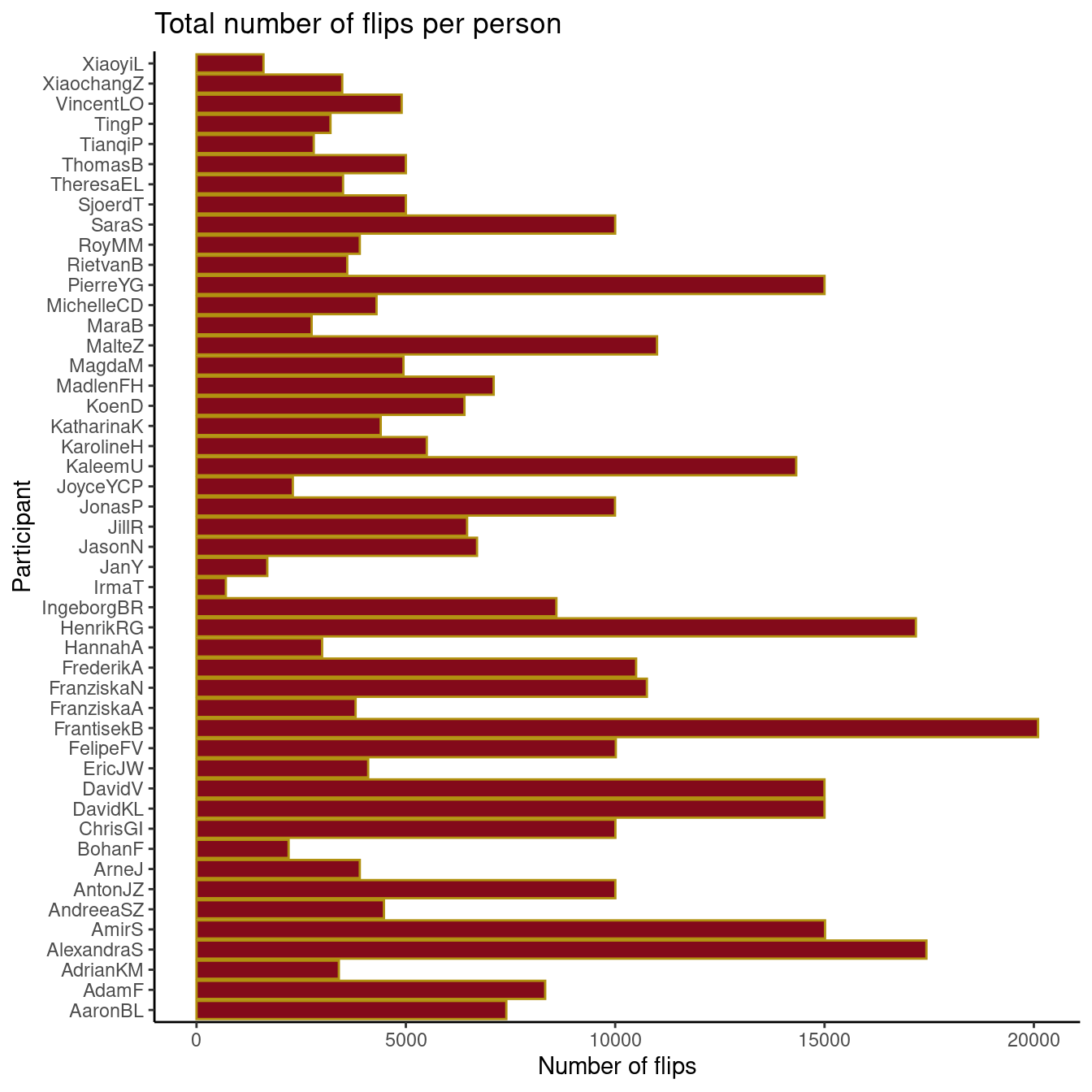
We don’t simulate fliping coins all the time…
Show the code
library(tidyverse)
flipsData <- flipsData |>
mutate(proportionSame = same / flips)
ggplot(flipsData, aes(x=proportionSame)) +
geom_density(fill = "#00609C", alpha = 0.3)+
geom_histogram(color = "#B19110",
fill= "#830A1A",
bins = 10)+
theme_classic()+
ggtitle("Histogram of proportions of times coin landed on the same side as where it started")+
ylab("Frequencies")+
xlab("Proportions")+
annotate("text", x = 0.56, y = 30, label = "Mean = 0.51, SD = 0.02")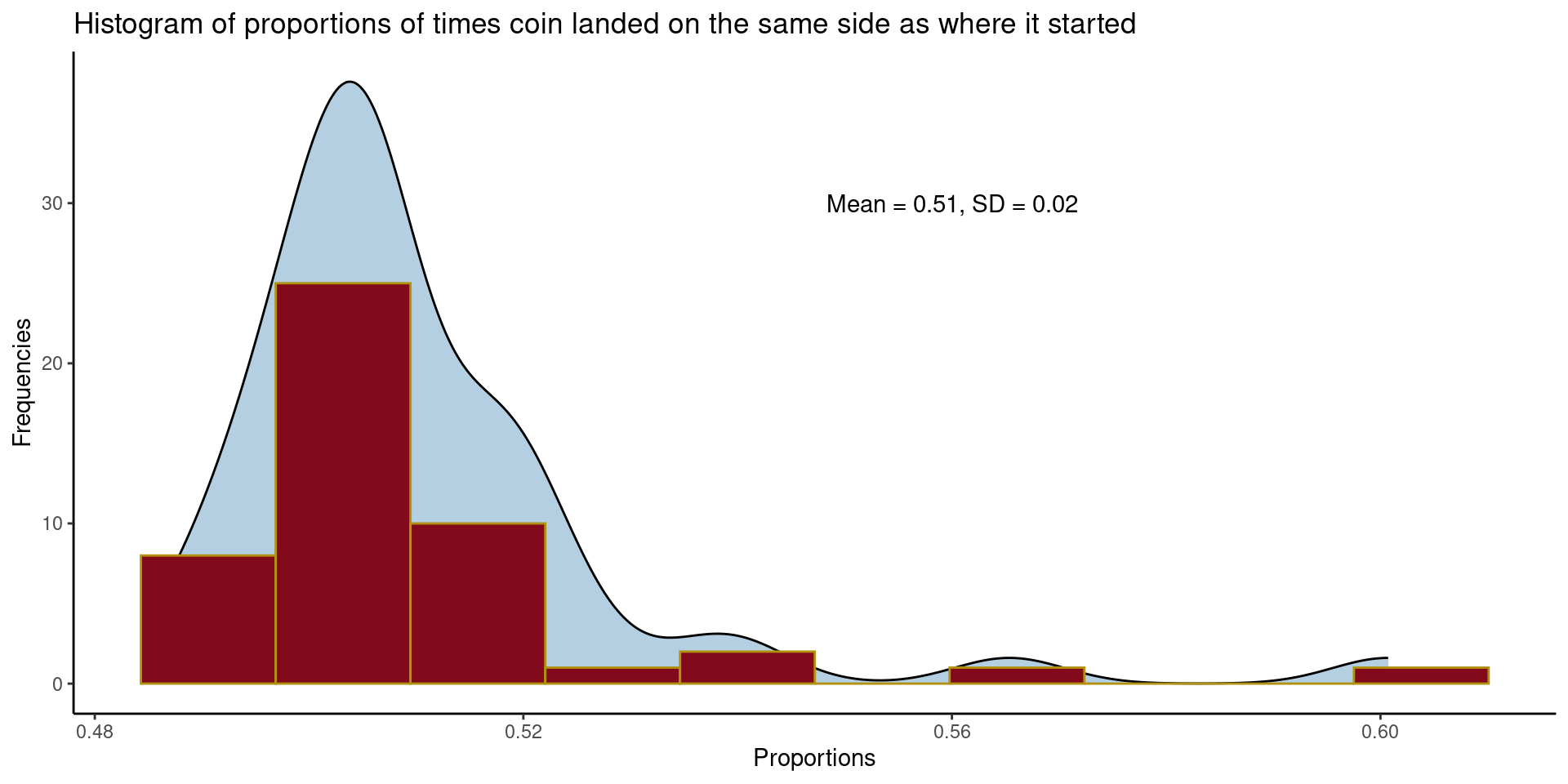
We can return to our simulations …

Simulation time! II
Hopefully, at this point the notion of DATA versus data starts to make sense.
I want to introduce another model that we might study further if time allows, this new model is the Poisson pdf, a.k.a Poisson distribution.
The function form of the Poisson distribution is:
Let’s untangle the formula:
- The symbol \(\lambda\) is the Greek letter “lambda”, it represents the theoretical average.
- The letter \(e\) is called Euler’s constant, its numerical value is approximately \(e = 2.71828...\). You might remember this symbol when you did exponential functions in high school or college. -The term \(y!\) is “y factorial” , you might remember factorials from high school or college, they are used a lot in probability. It can be defined as:
Simulation time! III
As always, it is not required to remember the Poisson formulation, but it is more important to understand how we can use this model to explain our observed data:
- Let’s imagine that you want to find a model to describe attendance in high school. We could try to generate data that assumes that a high school student has on average 8 absences.
Show the code
The mean is 7.98- Our model generated 300 observations, with an average number of absences = 7.98. It is likely that this number will be closer to 8 if you simulate more observations.
Simulation time! IV
The probability of each value in our tiny Poisson simulation can be represented in list form as:

- The Poisson pdf is a good model to represent counts such as the number of times you successfully wake up early and do exercise, the number of shoes, the number of family members in each household and many other counting variables.
Continuous Probability Distribution Functions
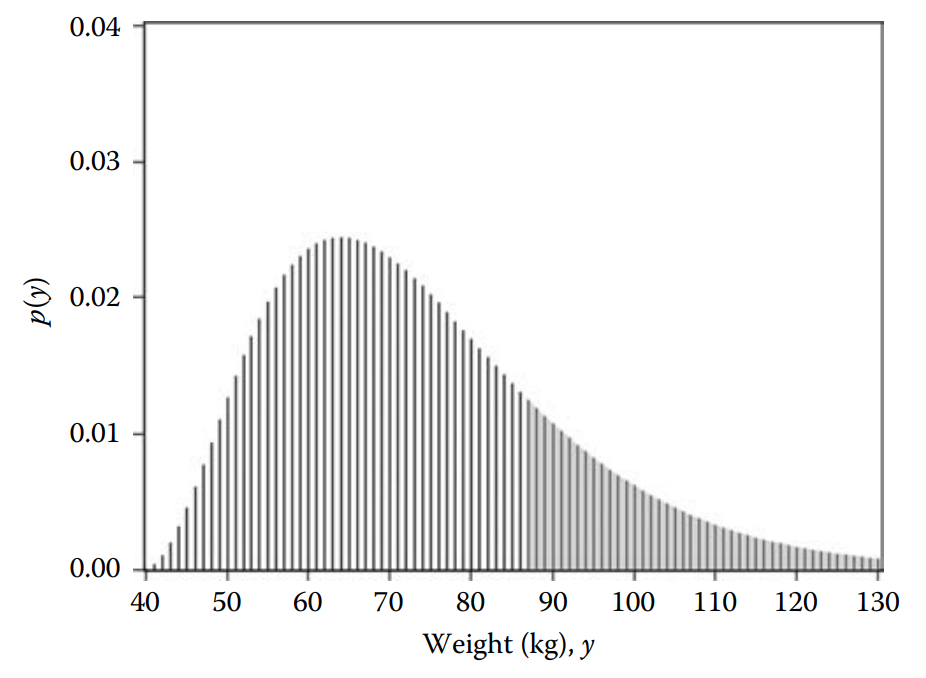
- Continuous distributions have several differences compare to discrete distributions.
- When the density plot corresponds to a continuous distribution, the \(y\)-axis does not show probability.
- When you estimate the density of continuous distribution you are estimating the “relative likelihood” For example, in this plot 50 kg has a likelihood of around 0.014, 55 kg has a likelihood of around 0.021. This means that is more likely to observe 55 kg compare to 50 kg.
Continuous Probability Distribution Functions II

Important: - The probability of a value in a density plot can only be estimated by calculating by estimating the area under the curve.
- The total area under the curve in discrete and continuous functions is always equal to 1.0.
Continuous Probability Distribution Functions III
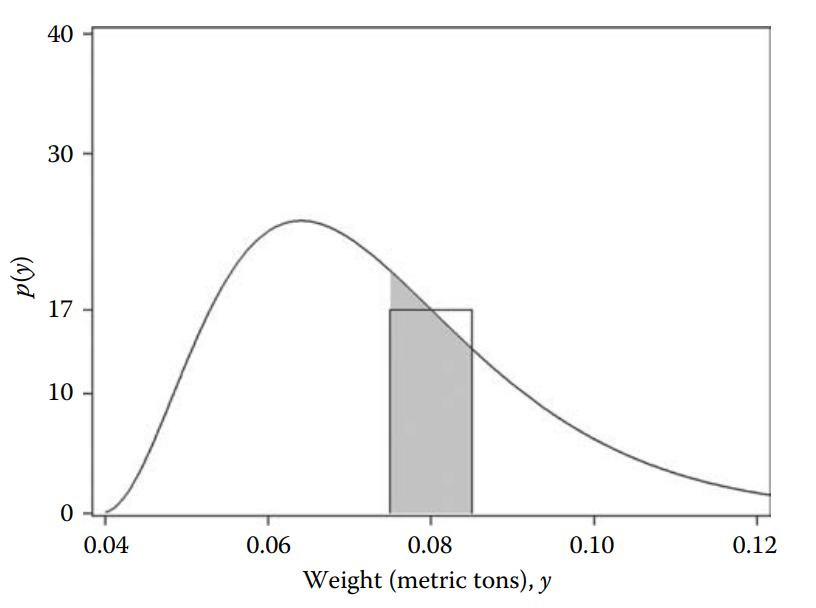
In this graph Westfall & Henning (2013) changed the metric from kg to metric tons.
This helps to show you how to estimate the probability of 0.08 metric tons from a density plot.
Then the probability of observing a weight (in metric tons) in the range \(0.08 \pm 0.005\) is approximately 17 × 0.01 = 0.17. Or in other words, about 17 out of 100 people will weigh between 0.075 and 0.085 metric tons, equivalently, between 75 and 85 kg.
But this is is just an approximation, integrals would give us the exact probability, but we will avoid calculus today.
Continuous Probability Distribution Functions IV
Requirements for a Continuous pdf
- The values on the \(y\)-axis are always positive, it means the likelihood is always positive.
- Given that the area under curve represents PROBABILITY, the total area is always equals to 1.0.
More distributions: normal distribution
At this point it looks a little bit esoteric and dark, I will untangle the components of the normal distribution formulation.
- The component \(\frac{1}{\sqrt{2\pi\sigma}}\) is what we call a constant, it is a fixed quantity. Every probability density function will have a constant. This constant number helps to make sure that the area under the curve of a distribution is equal to 1 (believe me this is true!).
The second component \(exp \left\{ \frac{-(y-\mu)^2}{2\sigma^2} \right\}\) is what is called kernel it is like the “core” of the area under the curve.
The third important component is \(p(y|\mu, \sigma^2)\), in this expression; \(y\) represents any numeric value, \(\mu\) represents the mean of the distribution and \(\sigma\) is the variance of the distribution. Now we can read this third component as “probability of any number given a mean, and a variance”
More distributions: normal distribution II
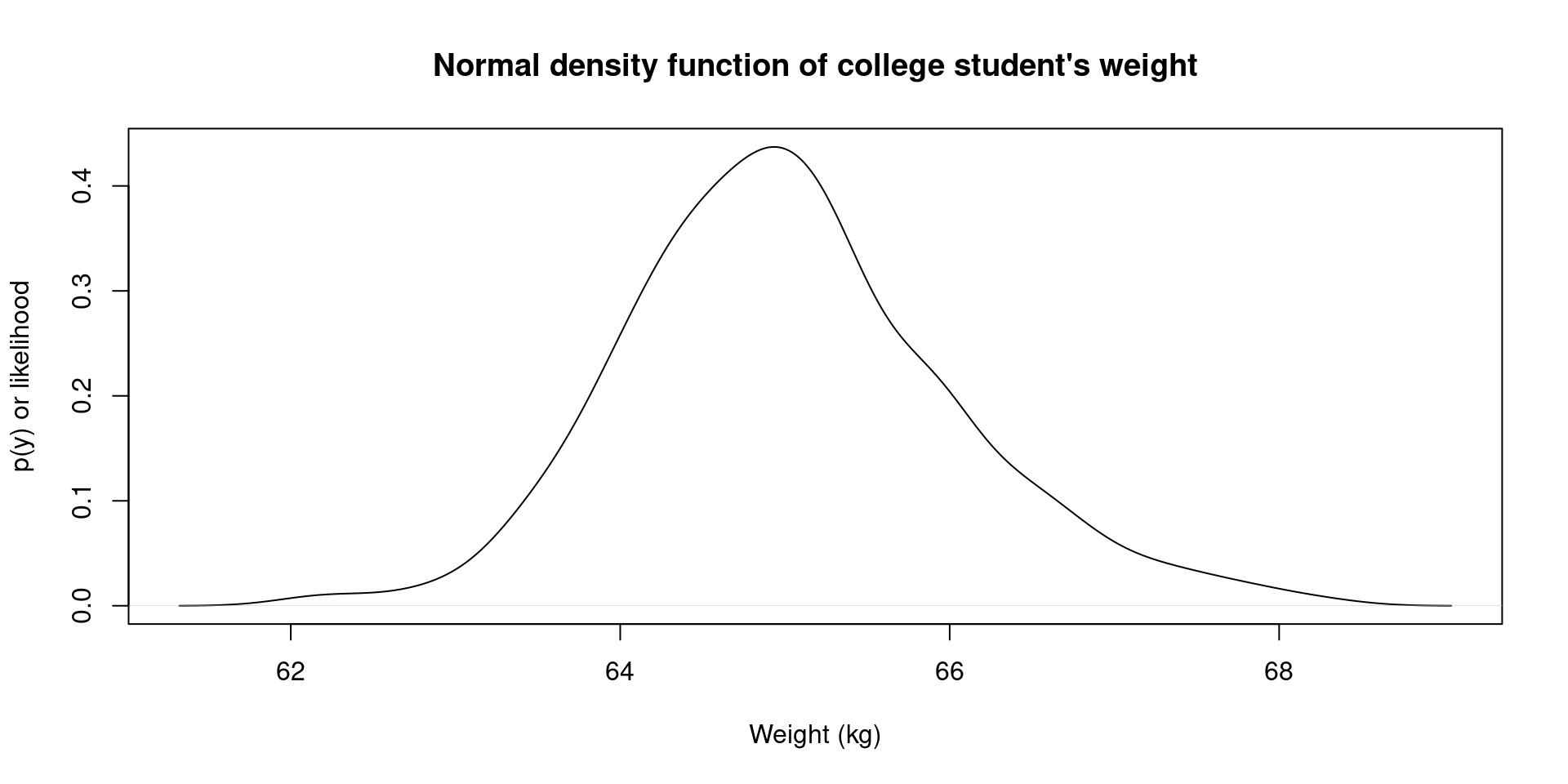
- As always, let me simulate some values using
R, imagine we need to find a model that best describes the weight distribution in College students. For this task, we could assume the normal distribution model with a mean of 65 kg and standard deviation equals to 1.0.
Show the code
[1] 65.90960 64.71476 63.83066 63.44413 65.46502 65.31280 66.48675 65.87327
[9] 64.84400 64.67924 62.12089 63.97994 64.42622 65.01382 64.85000 65.35106
[17] 64.86783 64.98873 64.54516 64.14890 63.47823 64.45281 66.13445 64.45036
[25] 65.66304 65.57285 62.93050 63.46320 63.99792 64.49344 65.89572 64.24975
[33] 65.90253 65.29621 65.85397 64.34964 65.16825 64.80732 65.56075 66.39590
[41] 65.68950 65.33977 64.06039 66.64493 64.47345 65.04675 65.85947 67.92296
[49] 66.34708 65.26185 64.95761 65.18777 64.03615 65.27033 65.84343 64.16392
[57] 65.61956 64.48135 67.40605 67.23284 65.12713 64.07411 63.98220 65.70498
[65] 64.88308 65.93083 64.72232 66.42429 65.23638 64.81533 66.98712 63.34341
[73] 64.93697 63.42742 65.41067 64.40579 64.70454 64.31235 65.16420 63.88185
[81] 64.43832 64.63143 64.33169 66.17669 65.05522 64.00396 65.43599 66.05379
[89] 65.39605 63.63870 66.18342 66.61002 65.84883 64.91560 65.79335 65.32865
[97] 65.93242 64.77581 64.21611 65.83586 67.52724 64.90828 64.33488 64.42051
[105] 65.95834 66.25977 64.91274 65.06262 64.47752 64.62498 65.13740 64.24417
[113] 65.36593 67.36820 65.70180 64.33536 65.96453 64.97927 68.24824 65.39837
[121] 64.00358 65.19193 64.43649 64.03446 63.96788 64.99354 64.32949 66.39454
[129] 65.46359 66.03655 64.66212 64.30517 64.21899 64.55146 63.81233 65.18873
[137] 65.30952 64.32071 65.17876 64.50110 64.66146 65.01361 64.74170 65.08205
[145] 64.42346 64.32447 65.23062 64.46689 66.69426 64.94310 65.24772 65.00605
[153] 63.93441 67.81550 64.76292 66.26200 64.15244 64.70025 65.06429 65.57770
[161] 63.39030 65.24833 64.62538 65.88314 64.93269 65.01867 64.83311 64.16538
[169] 65.08892 65.60057 65.15178 64.51507 64.65132 63.98354 64.43078 63.79769
[177] 64.79643 65.25849 63.31048 65.06860 64.70367 64.48503 64.58913 65.50374
[185] 62.96262 64.38087 66.59937 66.05083 63.79779 66.04224 64.68900 65.01352
[193] 64.49640 63.70097 63.88770 67.28460 66.72947 63.65179 65.44370 65.67320
[201] 65.26623 64.82400 64.67668 64.78615 64.89735 65.16560 64.86284 63.69684
[209] 64.36736 65.50050 64.68430 67.10004 65.13415 65.07864 65.75652 66.96074
[217] 64.67984 65.33965 64.32788 64.99155 63.72848 64.85579 64.81778 64.67416
[225] 66.54865 65.22833 65.81325 64.69429 66.10983 64.80612 63.39200 65.88671
[233] 64.01276 64.33288 63.46912 66.61400 64.11193 63.11924 64.71432 63.55637
[241] 65.91217 64.50794 64.35599 67.67487 66.97199 65.09739 66.49791 65.46359
[249] 65.92001 65.91692 63.40351 64.27549 66.08439 64.05049 65.84046 63.69535
[257] 64.29846 65.15456 63.72143 66.81415 65.73656 63.93622 63.74965 65.40493
[265] 64.74493 64.89682 64.95052 62.67580 65.33750 65.48994 64.24487 65.38974
[273] 66.34487 63.93986 66.39666 64.63785 65.39375 65.40279 65.28578 65.01735
[281] 66.74379 66.87585 64.91307 66.32705 64.25904 64.07473 65.96503 65.33417
[289] 63.96063 65.42224 62.30688 64.32297 66.52509 63.99097 64.86705 65.34434
[297] 64.17483 65.01194 64.99918 65.14846More distributions: normal distribution III
- We can check the density distribution of this sample that comes from the normal distribution model:
More distributions: normal distribution IV
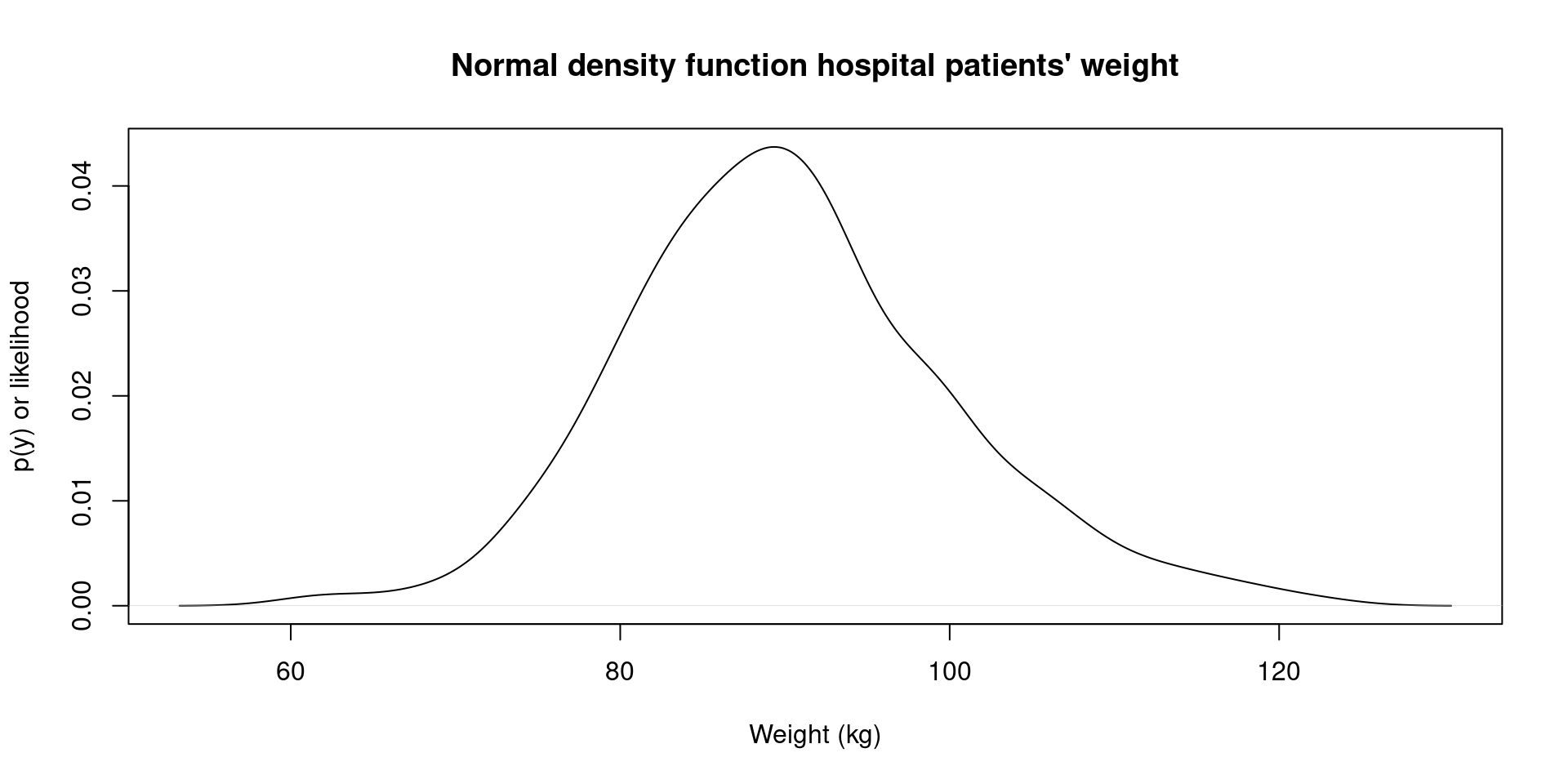
- We can also imagine that we need a model to describe the weight of hospital patients. But, this time probably, we will see more overweight individuals because of diverse health problems. Then, a mean = 65 kg is not realistic (143.3 lbs), probably we should assume a mean = 90 kg (198.42 lbs), and probably the observed data will be spread out, so we can use a larger values for the standard deviation, perhaps something around 10.
Show the code
[1] 99.09603 87.14758 78.30664 74.44127 94.65025 93.12797 104.86753
[8] 98.73265 88.43998 86.79235 61.20891 79.79938 84.26221 90.13819
[15] 88.49998 93.51056 88.67827 89.88726 85.45157 81.48895 74.78235
[22] 84.52814 101.34451 84.50357 96.63045 95.72855 69.30499 74.63198
[29] 79.97919 84.93441 98.95721 82.49745 99.02532 92.96213 98.53972
[36] 83.49641 91.68247 88.07319 95.60747 103.95905 96.89498 93.39768
[43] 80.60386 106.44925 84.73451 90.46749 98.59471 119.22961 103.47075
[50] 92.61846 89.57613 91.87772 80.36150 92.70328 98.43425 81.63920
[57] 96.19561 84.81348 114.06050 112.32838 91.27126 80.74112 79.82199
[64] 97.04981 88.83082 99.30830 87.22319 104.24293 92.36383 88.15335
[71] 109.87124 73.43411 89.36973 74.27417 94.10665 84.05789 87.04545
[78] 83.12347 91.64199 78.81849 84.38325 86.31432 83.31688 101.76688
[85] 90.55224 80.03963 94.35986 100.53789 93.96049 76.38699 101.83422
[92] 106.10019 98.48829 89.15598 97.93345 93.28650 99.32421 87.75811
[99] 82.16114 98.35859 115.27235 89.08279 83.34876 84.20506 99.58339
[106] 102.59770 89.12740 90.62618 84.77518 86.24982 91.37400 82.44167
[113] 93.65933 113.68198 97.01798 83.35357 99.64534 89.79270 122.48244
[120] 93.98373 80.03576 91.91926 84.36490 80.34458 79.67885 89.93544
[127] 83.29487 103.94544 94.63586 100.36548 86.62125 83.05169 82.18990
[134] 85.51461 78.12330 91.88730 93.09520 83.20710 91.78756 85.01100
[141] 86.61460 90.13608 87.41698 90.82048 84.23460 83.24472 92.30620
[148] 84.66887 106.94258 89.43101 92.47715 90.06048 79.34405 118.15496
[155] 87.62915 102.61997 81.52439 87.00250 90.64290 95.77699 73.90302
[162] 92.48329 86.25377 98.83139 89.32694 90.18671 88.33110 81.65385
[169] 90.88921 96.00573 91.51776 85.15071 86.51324 79.83544 84.30776
[176] 77.97693 87.96432 92.58489 73.10476 90.68604 87.03665 84.85029
[183] 85.89134 95.03740 69.62624 83.80868 105.99374 100.50826 77.97789
[190] 100.42236 86.88997 90.13518 84.96399 77.00973 78.87698 112.84603
[197] 107.29474 76.51790 94.43699 96.73195 92.66227 88.23995 86.76681
[204] 87.86150 88.97352 91.65598 88.62836 76.96842 83.67362 95.00498
[211] 86.84302 111.00035 91.34154 90.78639 97.56522 109.60737 86.79841
[218] 93.39651 83.27879 89.91554 77.28481 88.55791 88.17783 86.74163
[225] 105.48651 92.28331 98.13252 86.94293 101.09826 88.06121 73.91998
[232] 98.86712 80.12760 83.32878 74.69121 106.14002 81.11932 71.19242
[239] 87.14321 75.56373 99.12171 85.07938 83.55992 116.74873 109.71989
[246] 90.97392 104.97909 94.63592 99.20012 99.16920 74.03514 82.75492
[253] 100.84388 80.50494 98.40457 76.95353 82.98457 91.54557 77.21432
[260] 108.14149 97.36556 79.36224 77.49653 94.04927 87.44927 88.96823
[267] 89.50524 66.75803 93.37497 94.89937 82.44871 93.89736 103.44874
[274] 79.39864 103.96662 86.37846 93.93755 94.02794 92.85782 90.17349
[281] 107.43790 108.75847 89.13072 103.27050 82.59045 80.74730 99.65032
[288] 93.34172 79.60634 94.22238 63.06883 83.22968 105.25093 79.90966
[295] 88.67048 93.44337 81.74835 90.11941 89.99179 91.48458More distributions: normal distribution IV
- We can check now the probability density function of our simulated hospital sample:
More distributions: normal distribution V
library(ggplot2) ### <- this is a package in R to create pretty plots.
dataMerged <- data.frame(
group =c(rep("College", 300),
rep("Hospital", 300)),
weight = c(data_1, data_2))
ggplot(dataMerged , aes(x=weight, fill=group)) +
geom_density(alpha=.25) +
theme_bw()+
labs(title = "College and Hospital Weight Density Function") +
xlab("Weight (kg)") +
ylab("p(y) or likelihood")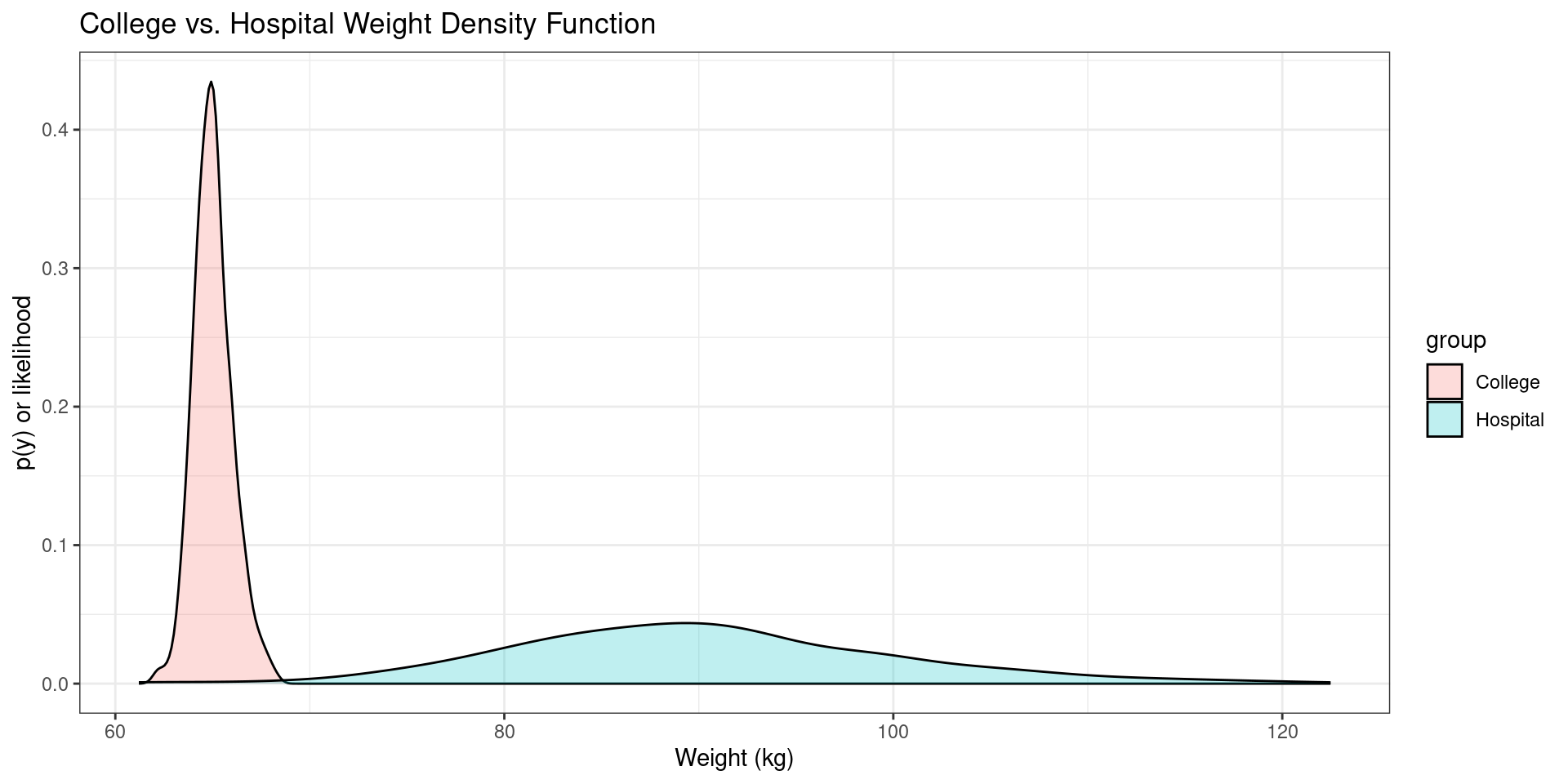
What is the main message here?
The main message is: Models produce data!
Remember we were talking about NATURE and DATA (uppercase)?
- Our statistical model (e.g. normal distribution) is our approximation to DATA, we create models that will generate observed data. That’s why in simulations sometimes our model is called “population model”, and from our data generating model we produce observed data.
Remember when we talked about random variables vs. fixed quantities?
- When we refer to the DATA (population model) the variables are random, but when we generate data like we did in
Rthat data are fixed quantities similar to collect data on campus related to dating strategies, once you collect your data, those numbers are fixed quantities that were generate by a natural process (data generating process). We cannot control the natural process like we do in simulation.
- When we refer to the DATA (population model) the variables are random, but when we generate data like we did in
We reduce uncertainty when we add more observations. We will study more about it in the next classes.
References

