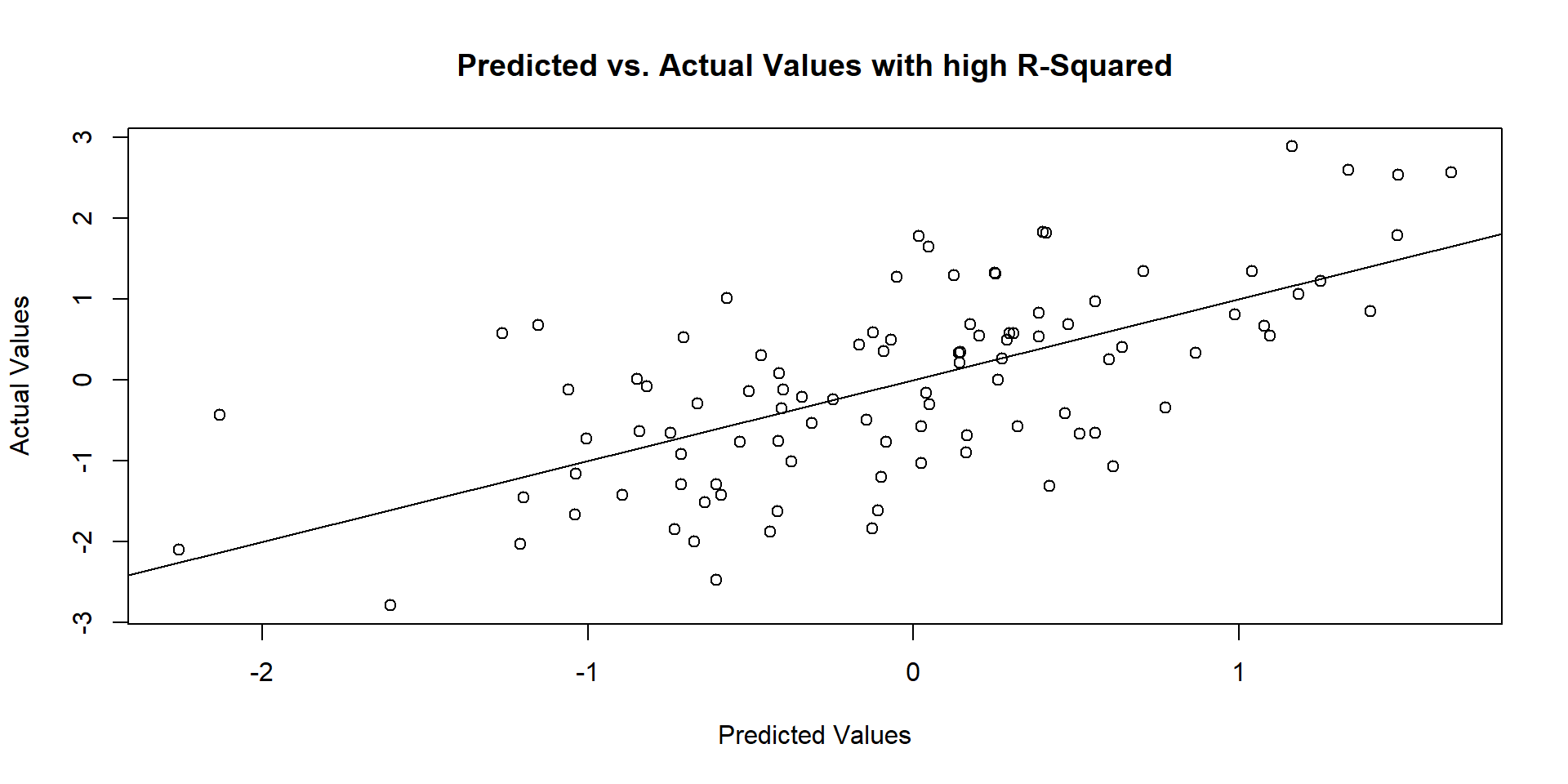
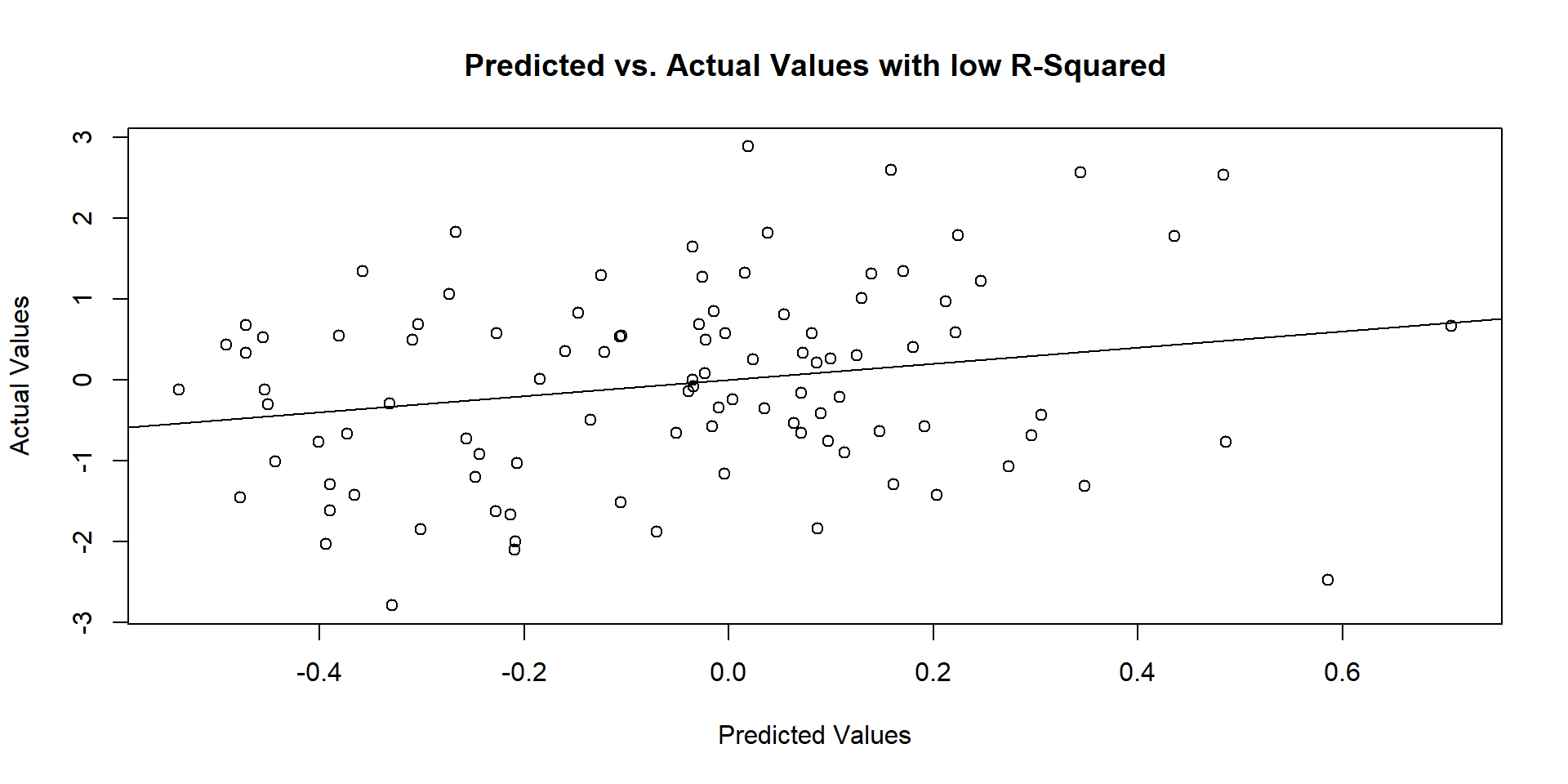
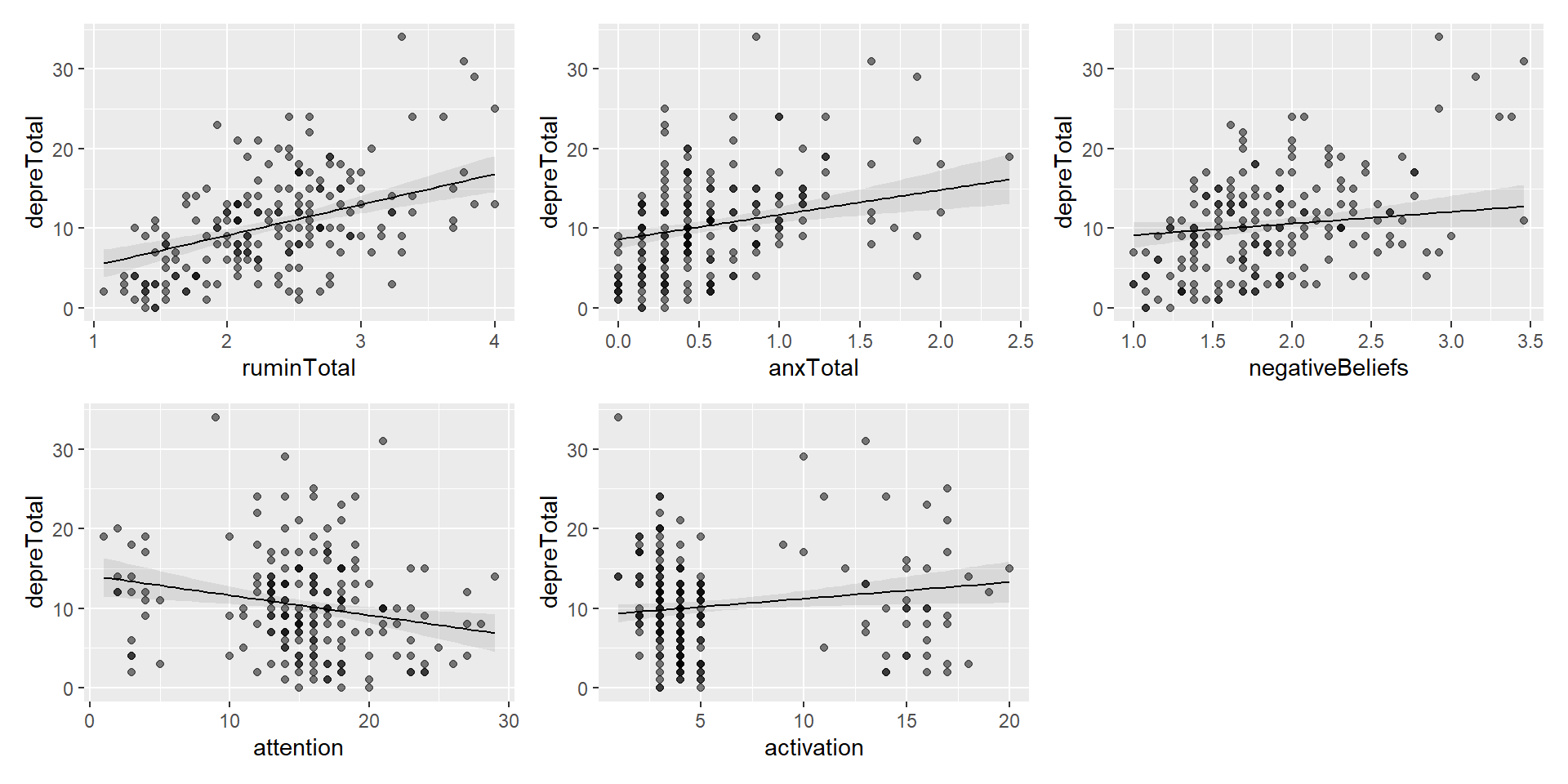
Show the code
### Simulation time!!
library(lavaan) ## <--- package to generate the values.
library(broom)
mod1 <- 'depression ~ 0.5*selfSteem + 0.8*rumination + 0*numberCandies'
generated <- simulateData(mod1,
meanstructure = TRUE,
sample.nobs = 100,
seed = 12)
fitModel <- lm(depression ~ selfSteem +
rumination +
numberCandies,
data = generated)
gt(tidy(fitModel),
rownames_to_stub= FALSE) |>
fmt_number(decimals = 2)- 1
- I’m specifying the “population model”.
- 2
- This line creates the simulated values. I’m generating 100 random values.
- 3
-
Estimating the model using function
lm().
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | −0.04 | 0.09 | −0.41 | 0.68 |
| selfSteem | 0.37 | 0.10 | 3.80 | 0.00 |
| rumination | 0.75 | 0.10 | 7.81 | 0.00 |
| numberCandies | 0.03 | 0.09 | 0.28 | 0.78 |