Norms and Basic Statistics for Testing

Gentle introduction

Esteban Montenegro-Montenegro, PhD

Department of Psychology and Child Development

Aims in this lecture

Explain relevant statistical concepts.
Describe and explain what is “norms”.
Perhaps more memes…

Why do we need stats when creating measurements ?

There are many reasons to implement statistical models in measurement theory.
- We need to create statistical models that help to understand Nature.
- In order to understand Nature we need to create instruments and measurements.
- The best way to create measurements is to create a model where observation and theory are linked together. In this step, statistics will help us to evaluate a model or multiple measurement models.
- Statistics will help to make inferences based on our observed data.
- You can describe the performance of groups, or describe traits with aggregated data.
- You can compare individuals and groups based on scores.

Wait… what is a statiscal model ?

To study and understand Nature we must construct a model for how Nature works.
A model helps you to understand Nature and also allows you to make predictions about Nature. There is no right or wrong model; they are all wrong! But some are better than others.

Models have Parameters

A parameter is a numerical characteristic of the data-generating process, one that is usually unknown but often can be estimated using data.

\[\begin{equation} Y \sim \beta_{0} + \beta_{1}X \end{equation}\]

For instance, in the model showed above, we have two unknown parameters, this model produces data $Y$. The unknown parameters are represented with greek letters, for instance the letter beta in the example above.

Mantra

Model produces data.
Model has unknown parameters.
Data reduce the uncertainty about the unknown parameters.

Types of Scales

Nominal: numerical values representing labels or groups. For example: marital status, job position, gender.
Ordinal: This scale allows you to rank individuals or objects but not to say anything about the meaning of the differences between the ranks. Likert scales are a good example.
Ratio: it is a scale with a meaningful zero. For example the Kelvin scale to measure temperature.

Now more stats!

Descriptives a probability distributions

You are probably familiar with frequencies. When reporting frequencies, we count how many times a value is repeated in your observed data.
In the next example I’ll show descriptive information related to a validation I did in Costa Rica.
My aim was to know how people felt when reading different adjectives and nouns. I asked to my participants to rate the perceived “arousal” and perceived “valance” of each word.
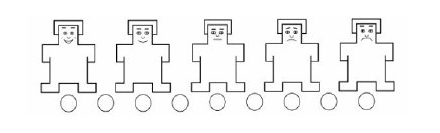
I utilized mannequins to evaluate valance:

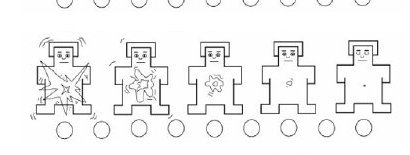
I used the following scale to measure arousal:

I didn’t create these scales, the original authors are Bradley & Lang (1994), an it was called The Self-Assessment Manikin. I thought it could be a good option to measure words’ positive and negative valence along with the “arousal”.
Each little individual scale had a number in my data set, the first little guy in each scale was coded as “9” and the last little individual was coded as “1”.
This means I utilized an ordinal scale where 9 represents “very positive word”, and 1 represents “very negative word”. Likewise, in the arousal scale 9 represents “strongly activated” whereas 1 represents “calm or not activated”.

SAM instrument

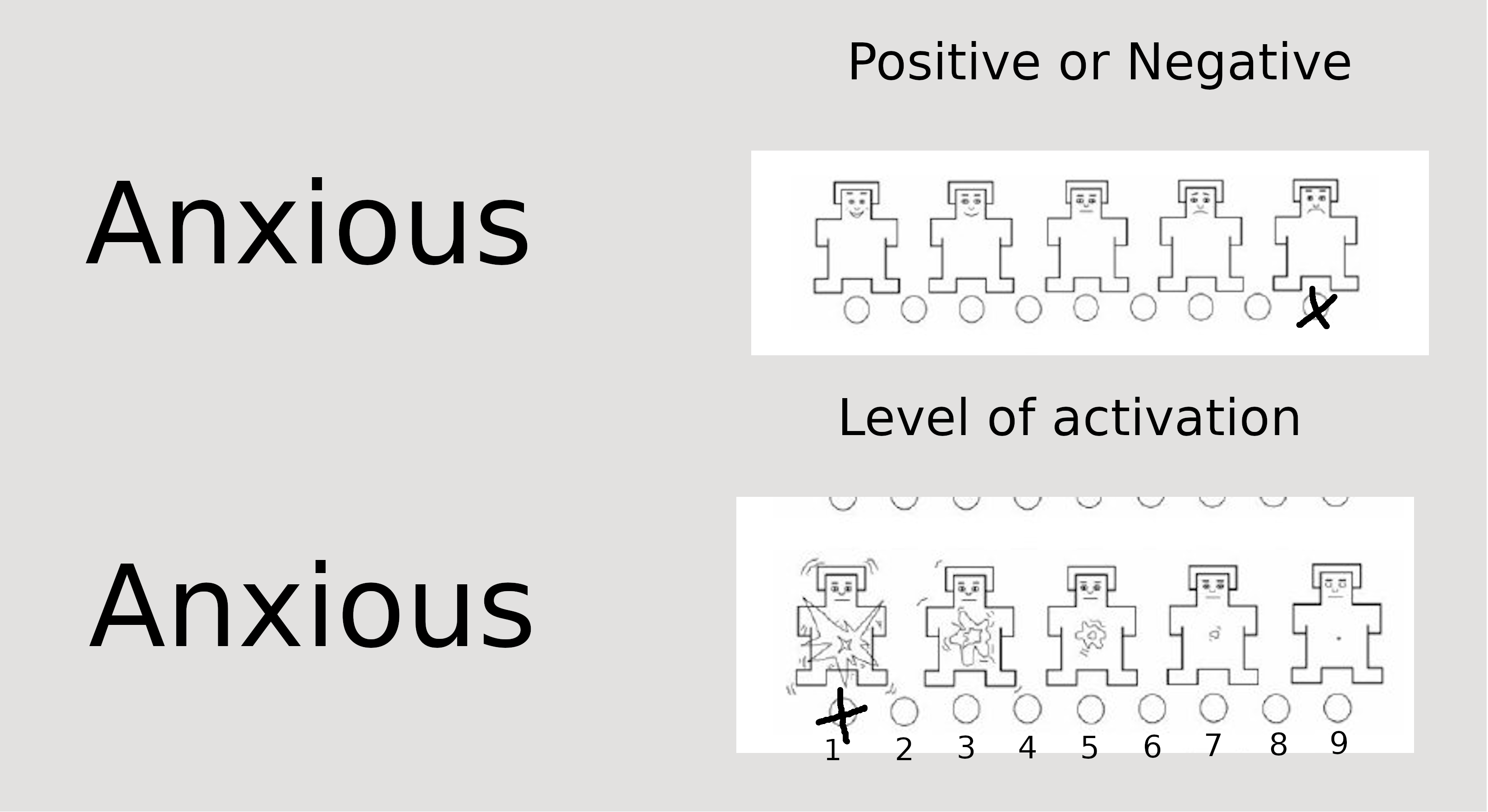
In this example a person marked rated “Anxious” “1” in valance and “9” in activation.

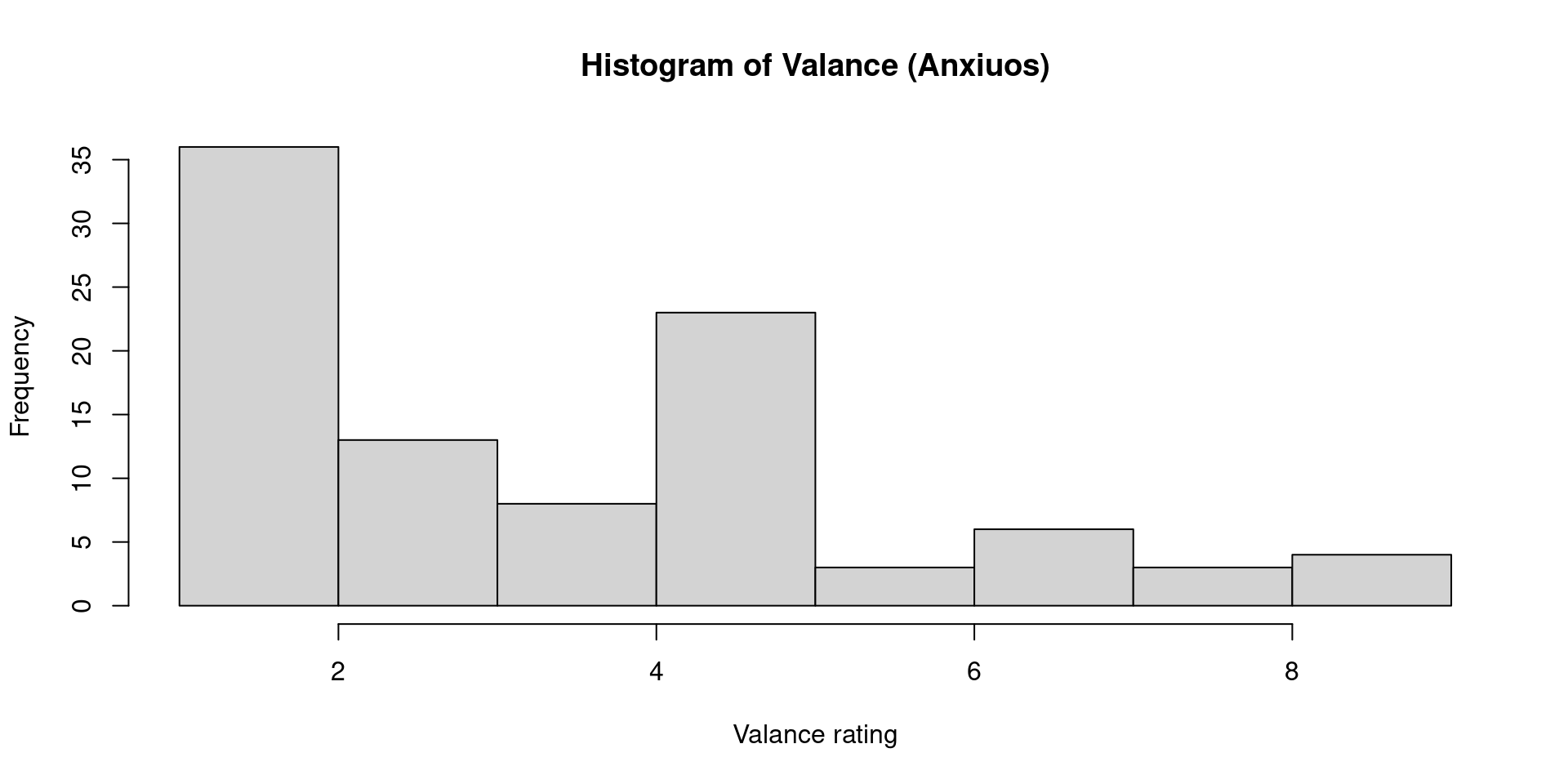
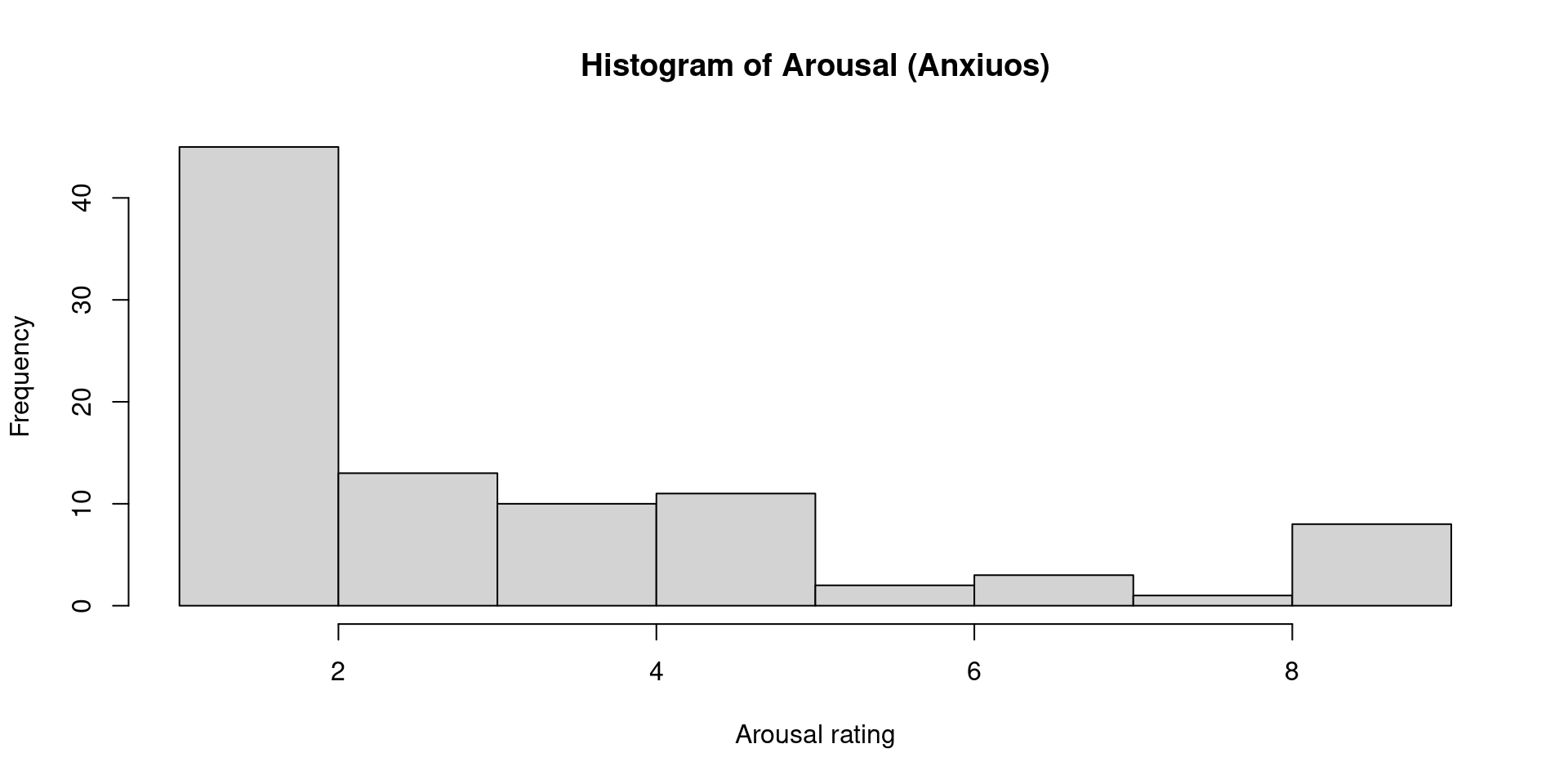
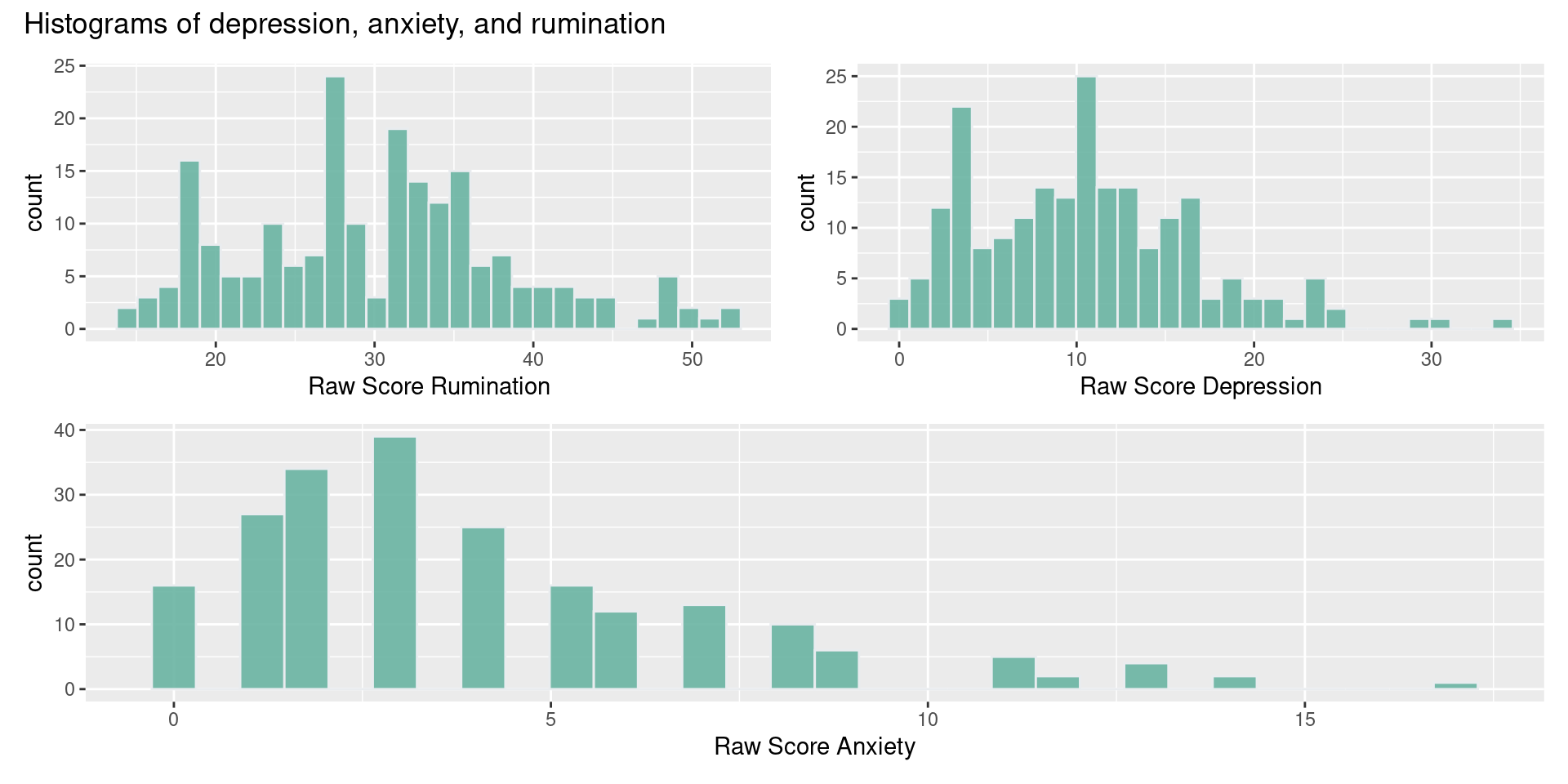
Let’s see some distibutions and frequencies

We can check a table

Frequencies of arousal and valance
Rating of Anxiuos
Response Options	Arousal	Valance
1	41	29
2	4	7
3	13	13
4	10	8
5	11	23
6	2	3
7	3	6
8	1	3
9	8	4
NA	7	4

Question

Did the participants understand what is “anxiety”?
Is it trivial to ask this question to ourselves?

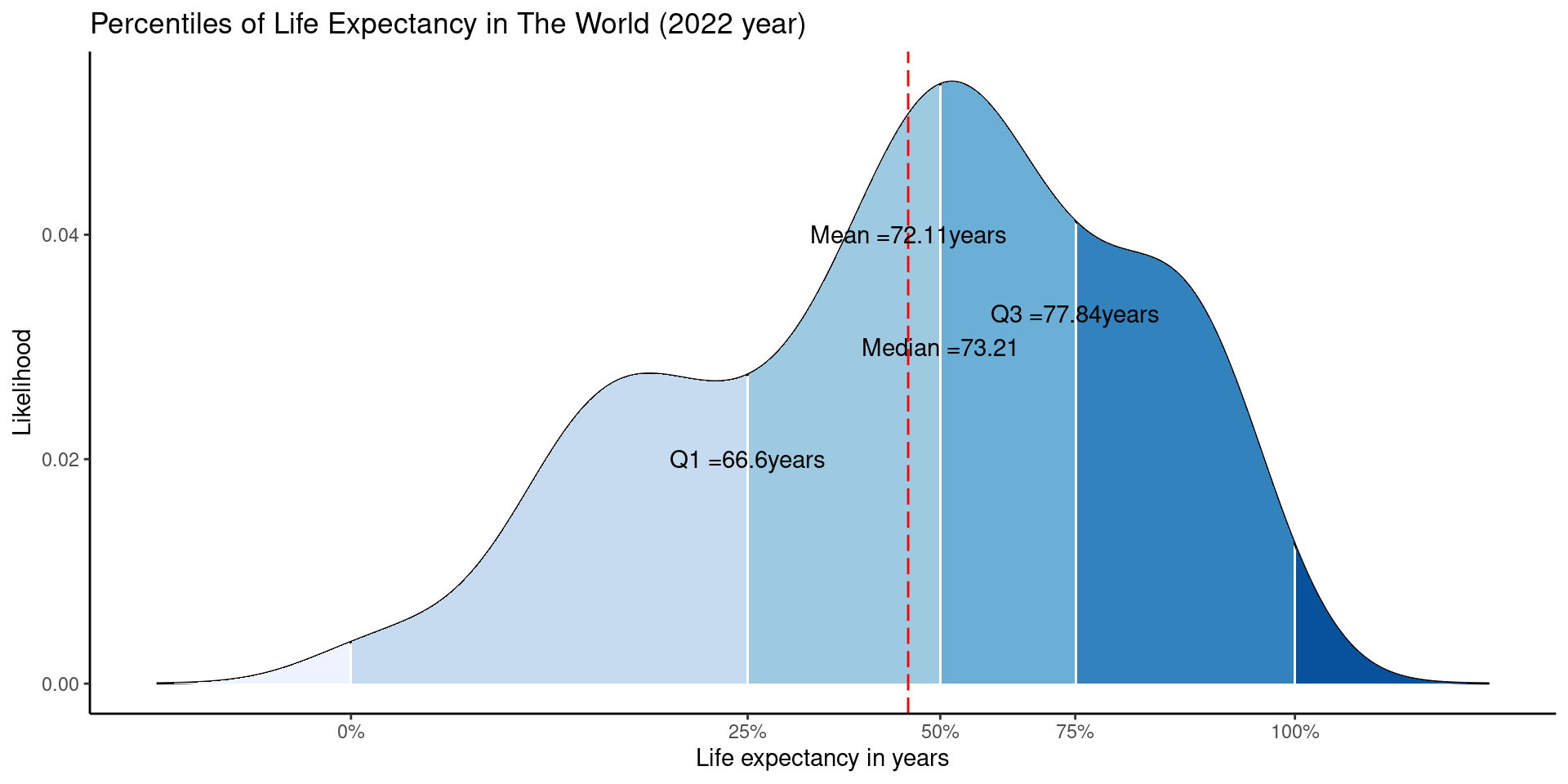
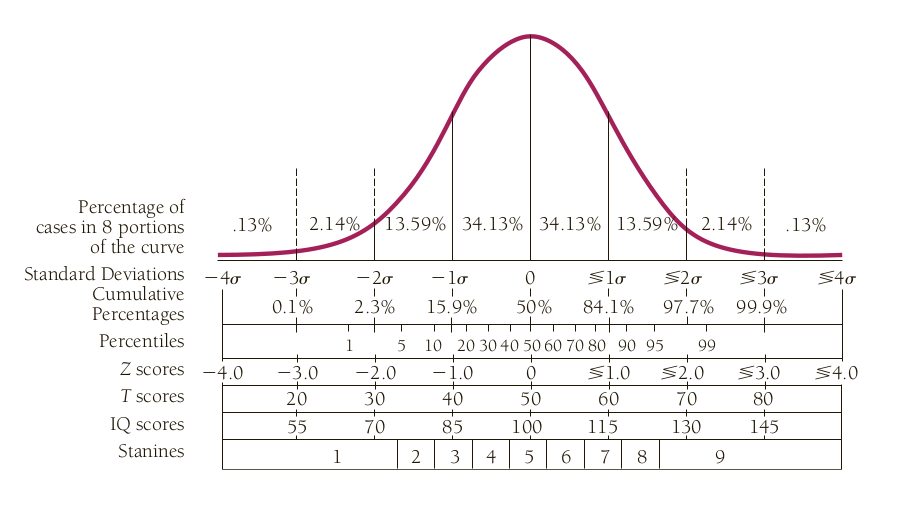
Percentiles

You can describe a distribution in terms of percentiles.
Let’s imagine the folllowing numbers represent households income:

$25,500\| $32,456\| $37,668\| $54,365\| $135,456

Now, we can follow this formula to estimate our percentiles (Westfall & Henning, 2013):

\[\begin{equation} \hat{y}_{(i-0.5)/n} = y_{(i)} \end{equation}\]

The little hat $\hat{}$ on top of $y$ means “estimate of”, this is used in statistics to comunicate that you are estimating a value from “data” (lowercase). This means you are estimating a value from your observed fixed data. The right-hand side is the $ith$ ordered value of the data, all together we can read the formula as:

The $(i − 0.5)/n$ quantile of the distribution is estimated by the $ith$ ordered value of the data

We can see an example:

Quantile example
$i$	$y(i)$	($i$-0.5)/$n$	\[\hat{y}_{(i-0.5)/n} = y(i)\]
1	25500	(1-0.5)/5 =0.10	25500
2	32456	(2-0.5)/5 =0.30	32456
3	37668	(3-0.5)/5 =0.50	37668
4	54365	(4-0.5)/5 =0.70	54365
5	135456	(5-0.5)/5 =0.90	135456

Then, we can say in plain English: “The 70th percentile of the distribution is measured by $54,365”.
Now notice something, why we don’t have data representing the 75th percentile?
Given that these are estimates , these numbers are approximations to the true value, If you collect more data you’ll have data in different percentiles, also more precision to capture the real value.

Percentiles

Source: CLICK HERE

Mean and Standard deviation

The mean or average is the most frequent estimate in testing and statistics, along with the standard deviation.
Let’s see their anatomy

Mean estimation:

\[\begin{align} \bar{X} &= \frac{\sum X}{n}\\ &= \frac{18+21+24+23+22+24+25}{7}\\ &= \frac{157}{7}\\ &= 22.43\\ \end{align}\]

Variance:

\[\begin{equation} s^2 = \frac{\sum (X_{i} - \bar{X})^2}{n-1} \end{equation}\]

Standard Deviation:

\[\begin{equation} s = \sqrt{\frac{\sum (X_{i} - \bar{X})^2}{n-1}} \end{equation}\]

Variance and SD

The standard deviation and variance are similar, they both measure the distance from the mean, but the standard deviation is a standardized measure, instead variance is scale dependent.

Mean and Standard deviation

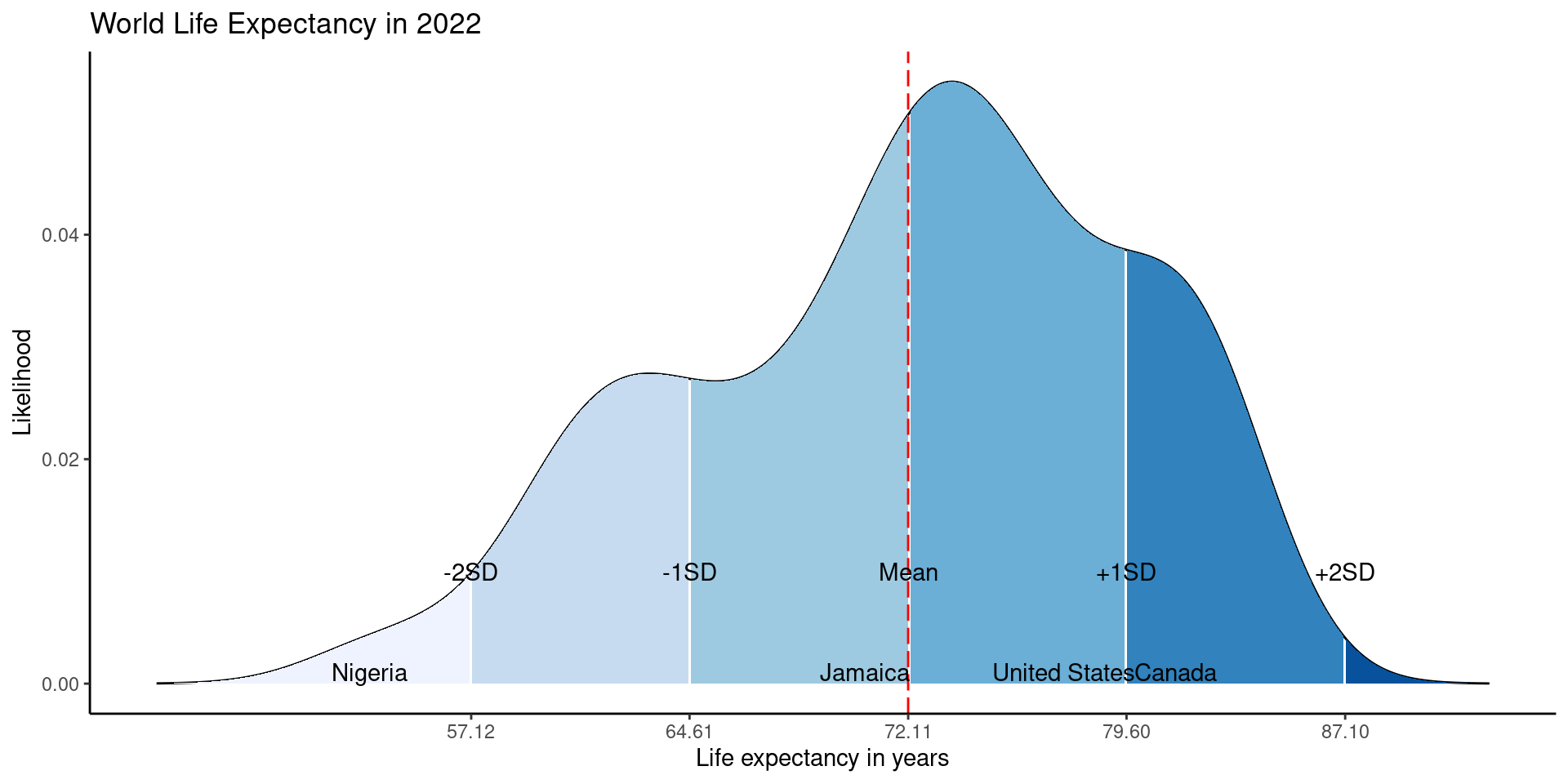
Z-Scores

Z Scores are used to compare observed scores versus a normative score, or to compare scores from different scales with different metric.
Let’s see an example where we need to compare two scores, but the scores have different range of values:

Variable	N = 175
depressionTotal
Mean (SD)	10 (6)
Min, Max	0, 34
anxietyTotal
Mean (SD)	4.1 (3.3)
Min, Max	0.0, 17.0
ruminationTotal
Mean (SD)	30 (8)
Min, Max	14, 52

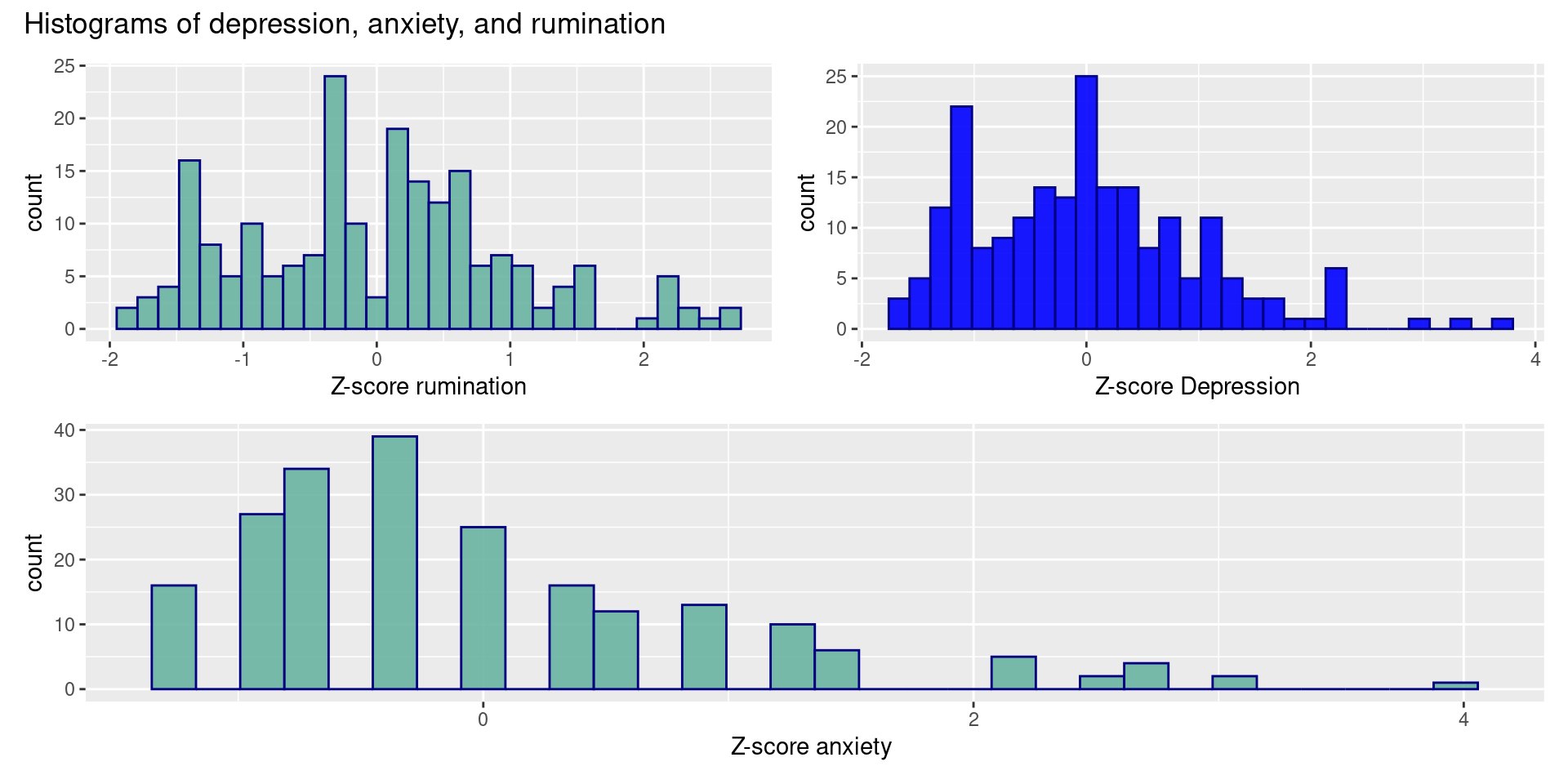
We’ll need to compute Z scores in these cases using the following transformation:

\[Z = \frac{X_{i}-\bar{X}}{SD}\]

In this transformation we estimate the distance from the mean ($\bar{X}$) for each observed value $X_{i}$, and then we divide it by the score’s standard deviation ($SD$).

Z-Scores

After tranforming the observed values, we can now compare distributions:

Variable	N = 175
depreZ
Mean (SD)	-0.01 (1.00)
Min, Max	-1.65, 3.72
anxietyZ
Mean (SD)	0.00 (1.02)
Min, Max	-1.26, 3.97
rumiZ
Mean (SD)	0.00 (1.00)
Min, Max	-1.93, 2.59

Norms and Norming

References

Bradley, M. M., & Lang, P. J. (1994). Measuring emotion: The self-assessment manikin and the semantic differential. Journal of Behavior Therapy and Experimental Psychiatry, 25(1), 49–59.

Westfall, P. H., & Henning, K. S. (2013). Understanding advanced statistical methods. CRC Press Boca Raton, FL, USA: