Correlation and Regression Models

Part 1

Esteban Montenegro-Montenegro, PhD

Psychology and Child Development

Today’s aims

To introduce correlation to estimate relationships between two variables.
To introduce the notion of covariance.
To study scatter plots to visualize correlations.

What is a correlation coefficient ?

A correlation coefficient is a numerical index that reflects the relationship between two variables. The value of this descriptive statistic ranges between -1.00 and +1.00.
A correlation between two variables is sometimes referred to as a bivariate (for two variables) correlation

What is a correlation coefficient ?

At the beginning we will study the correlation named Pearson product-moment.
There other types of correlation estimation depending on the data generating process of each variable.
Pearson product-moment deals with continuous DATA.

Correlation interpretation and other features

Salkind & Shaw (2020):

Correlation interpretation and other features (cont.)

Salkind & Shaw (2020):

A correlation can range in value from $-1.00$ to $+1.00$.
A correlation equal to 0 means there is no relationship between the two variables.
The absolute value of the coefficient reflects the strength of the correlation. So, a correlation of $-.70$ is stronger than a correlation of $+.50$. One frequently made mistake regarding correlation coefficients occurs when students assume that a direct or positive correlation is always stronger (i.e., “better”) than an indirect or negative correlation because of the sign and nothing else.
A negative correlation is not a “bad” correlation.
We will use the letter r to represent correlation. For example $r= .06$.

Correlation interpretation and other features (cont.)

$r_{xy}$ is the correlation coefficient.

$n$ is the sample size.

$X$ represents variable $X$.

$Y$ represents variable $Y$.

$\Sigma$ means summation or addition.

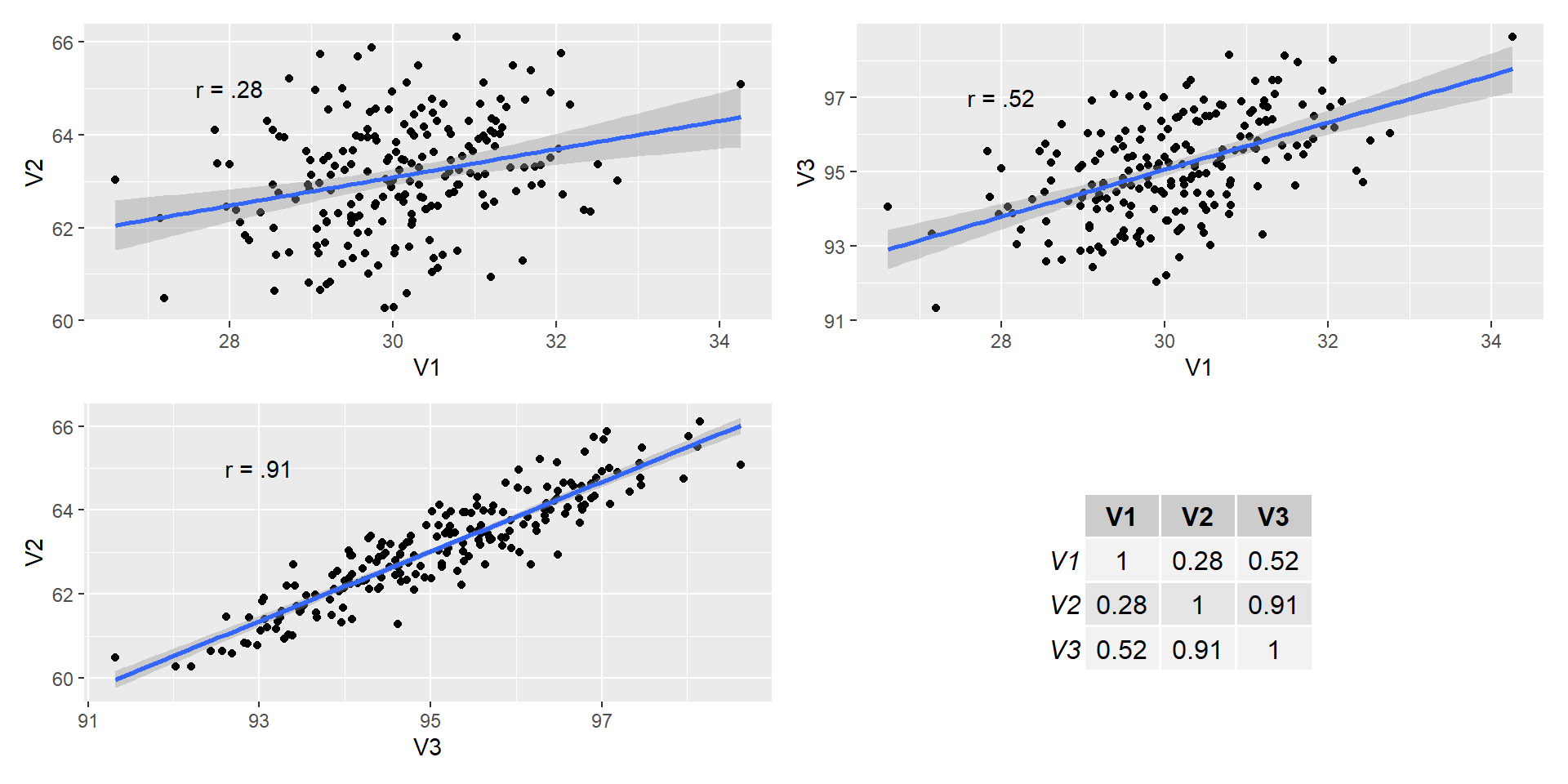
Let’s take a look at positive correlations

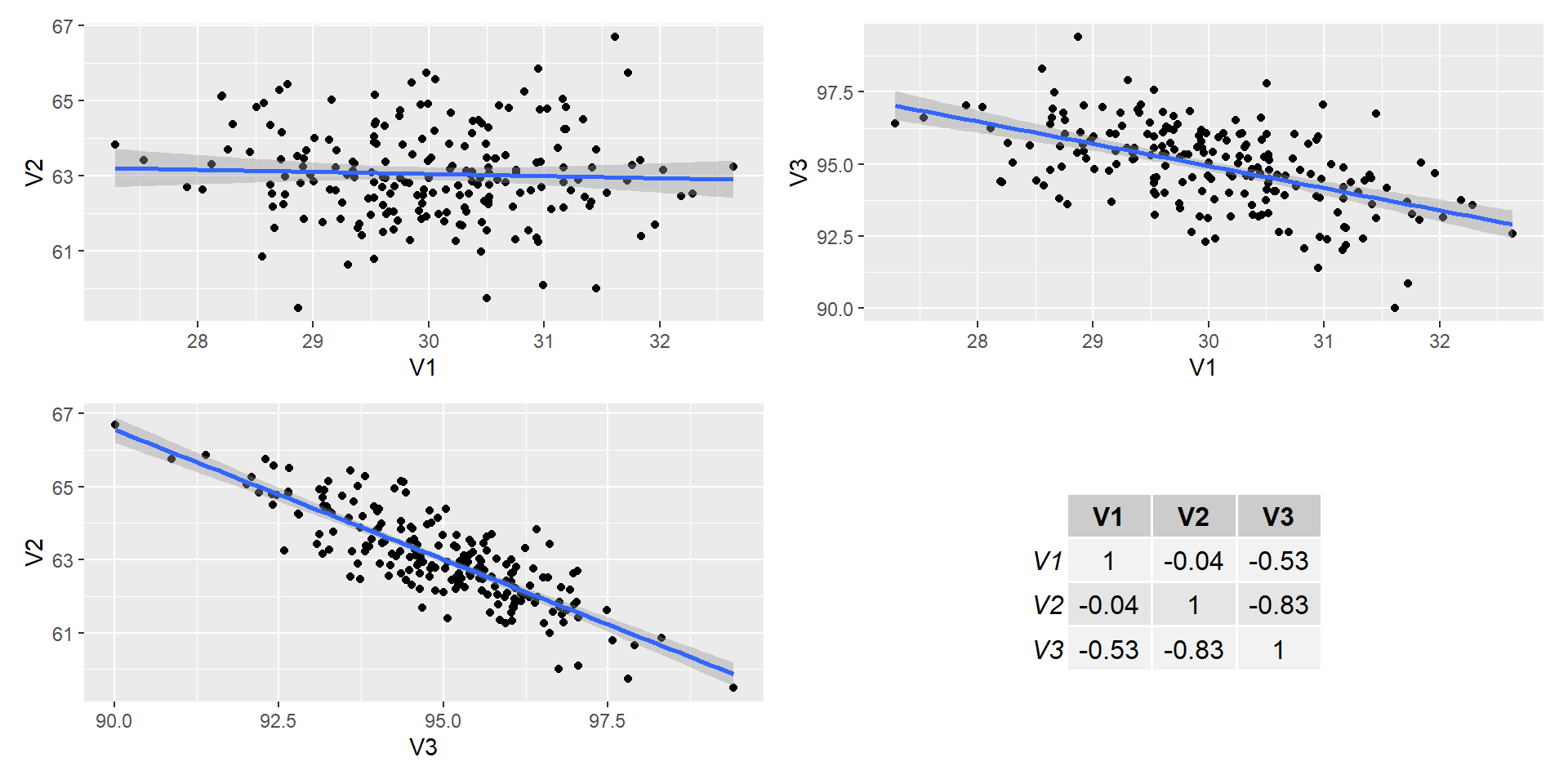
Let’s take a look at negative correlations (cont.)

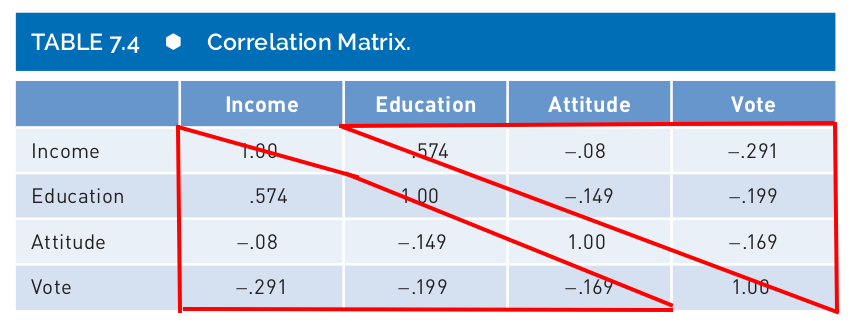
Correlation matrix

Salkind & Shaw (2020):

You will find a correlation matrix in publications.
It is the best way to represent several correlations between different pairs of variables.

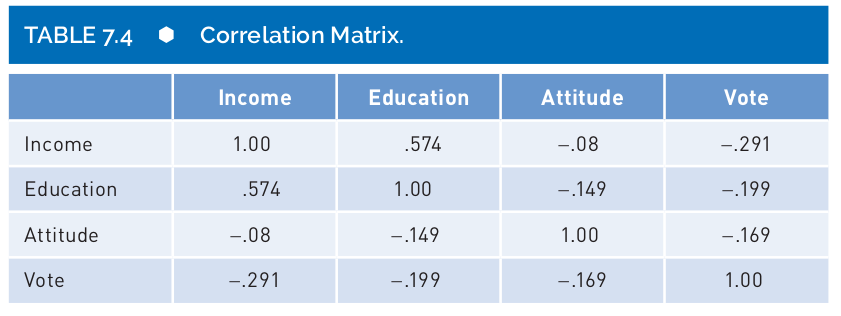
You will notice that a a correlation matrix has 1.00 on the diagonal and two “triangles” with the same information.

Coefficient of Determination

There is a useful trick, you could square your $r$ and get a measure of correlation in terms of percentage of shared variance:

Coefficient of Determination (cont.)

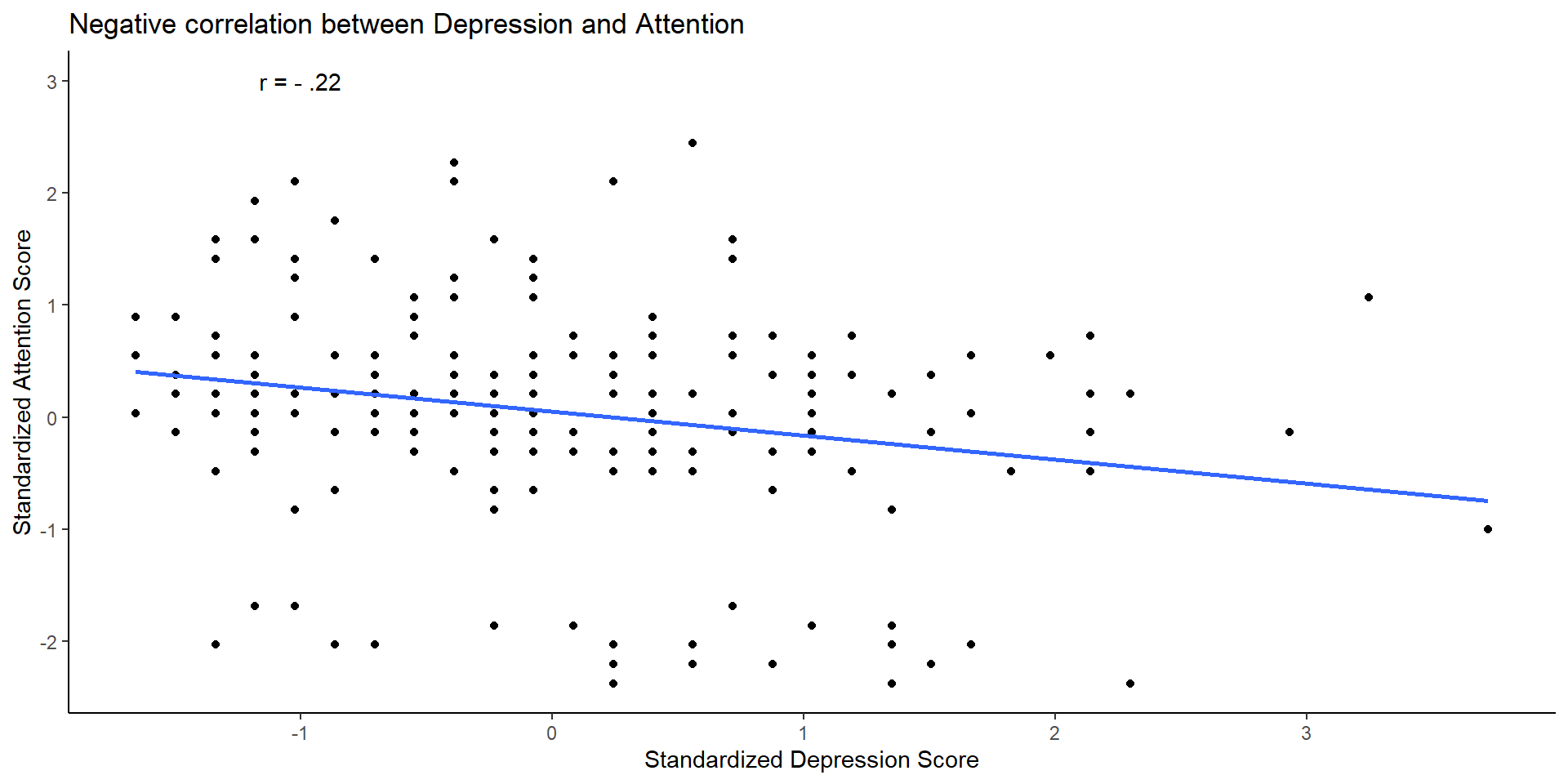
What is the coefficient of determination in this case?
We just need to estimate $ r^2= -0.22^2 = -0.05$. Attention and depression shared only 5$%$ of the variability (variance).

Scatter plots and direction of correlation

I have shown you several plots, these plots are called scatter plots.
These plots are useful to explore visually possible correlations.
When you create this plots, you only need to represent one of the variables in the x-axis and the other variable will be represented in the y-axis.

Note

Can you guess if the next scatter plot corresponds to a positive correlation?

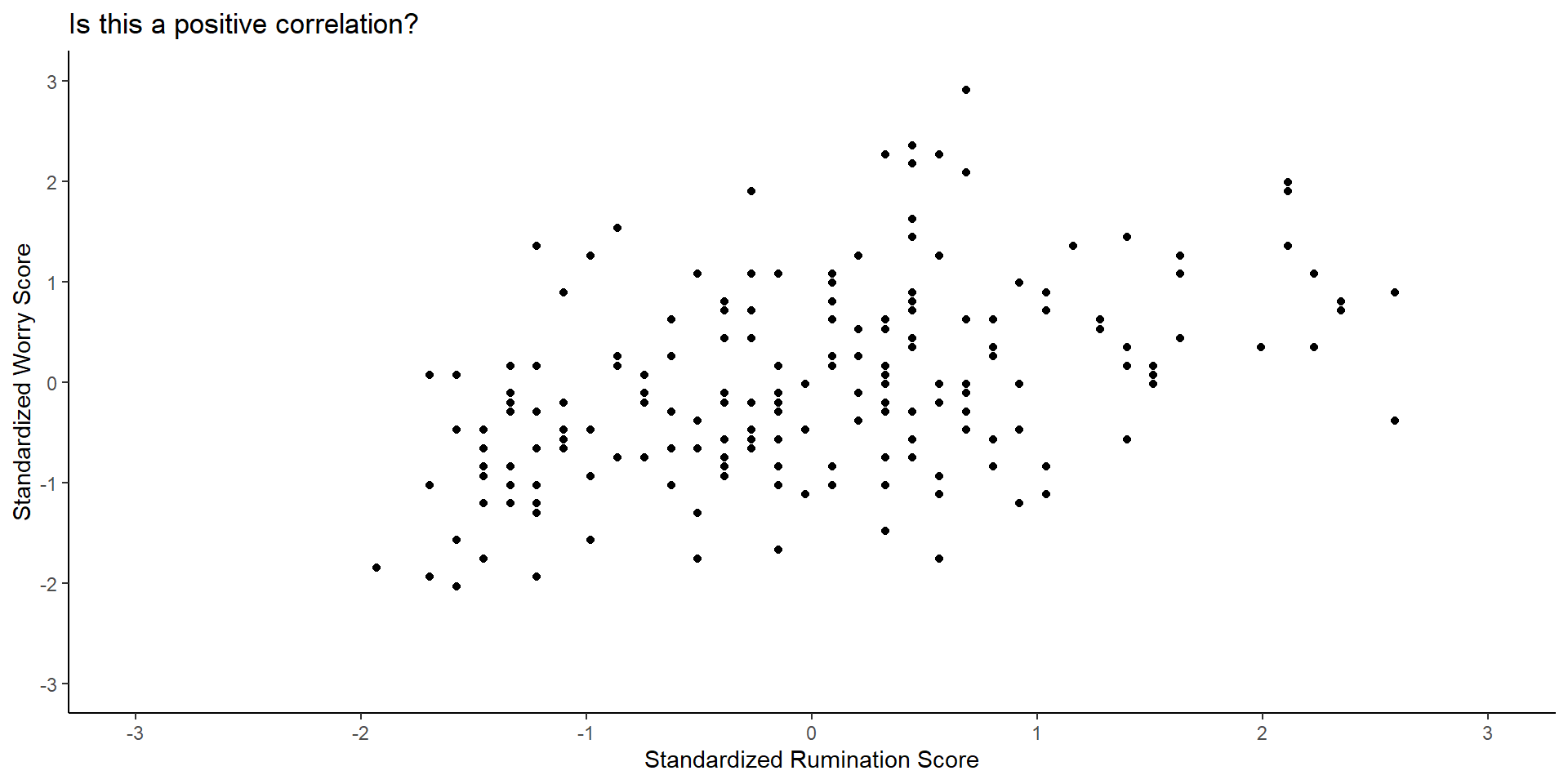
Scatter plots and direction of correlation (cont.)

We can check some values and see what is happening, like case #78, in the next plot:

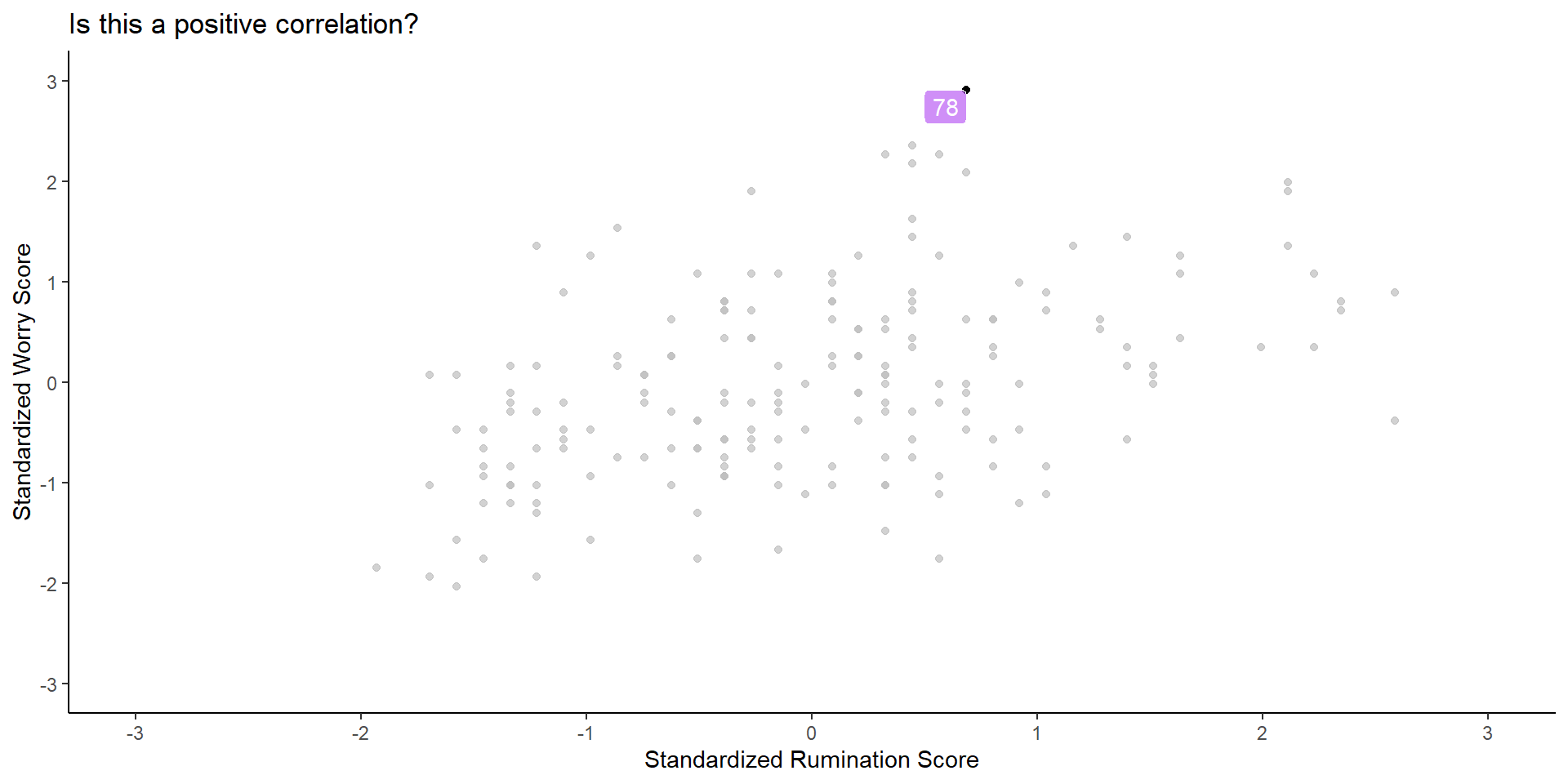
Scatter plots and direction of correlation (cont.)

Maybe if we add the line of best fit we will see it better:

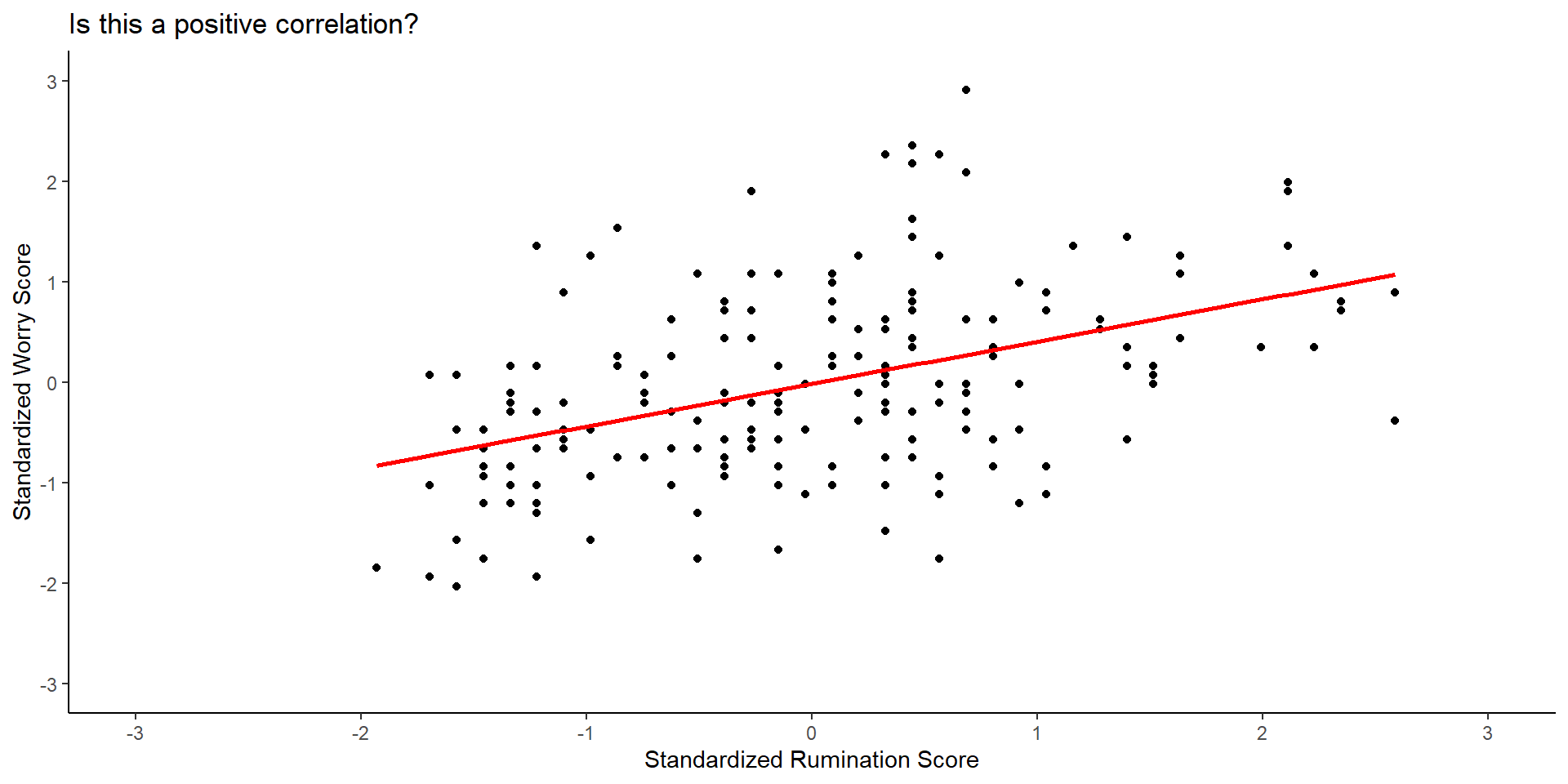
Scatter plots and direction of correlation (cont.)

Can you spot the direction of this correlation?
This data come from a questionnaire that asks to rate how emotional you feel. For instance, it asks: Rate how GREAT you feel where 1 = “not feeling” to 6=“I strongly feel it”.

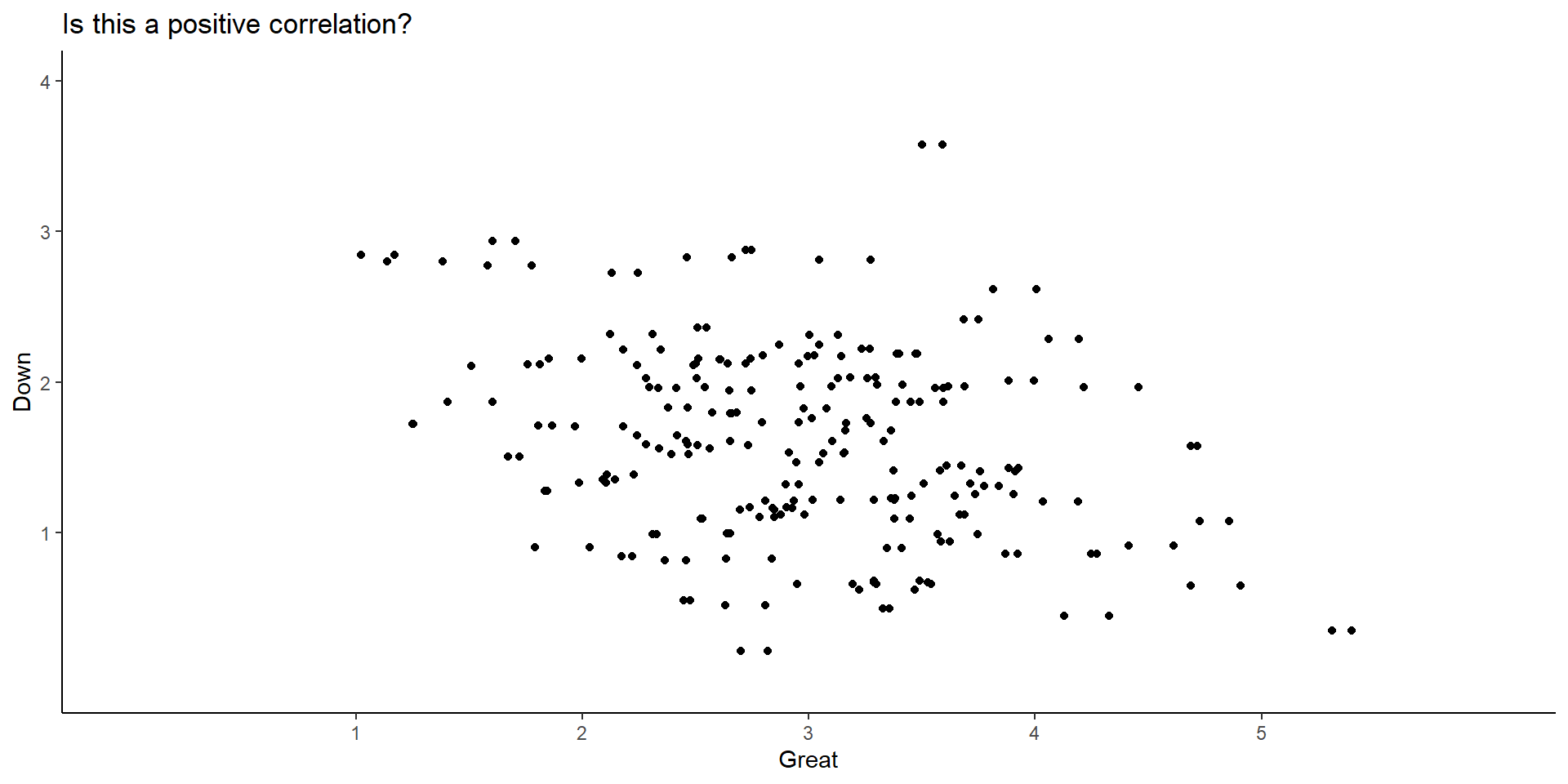
Scatter plots and direction of correlation (cont.)

Let’s add again the line of best linear fit:

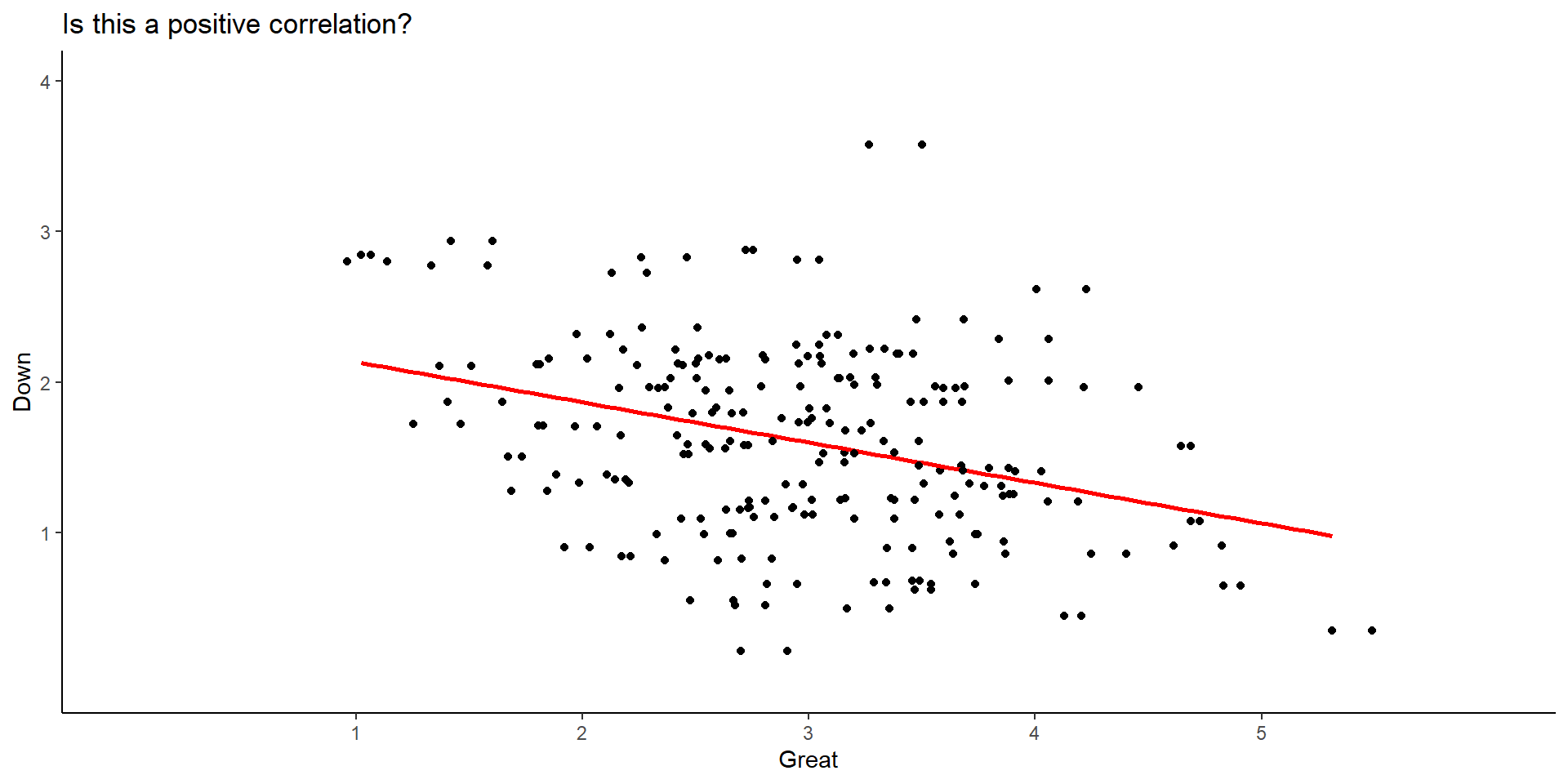
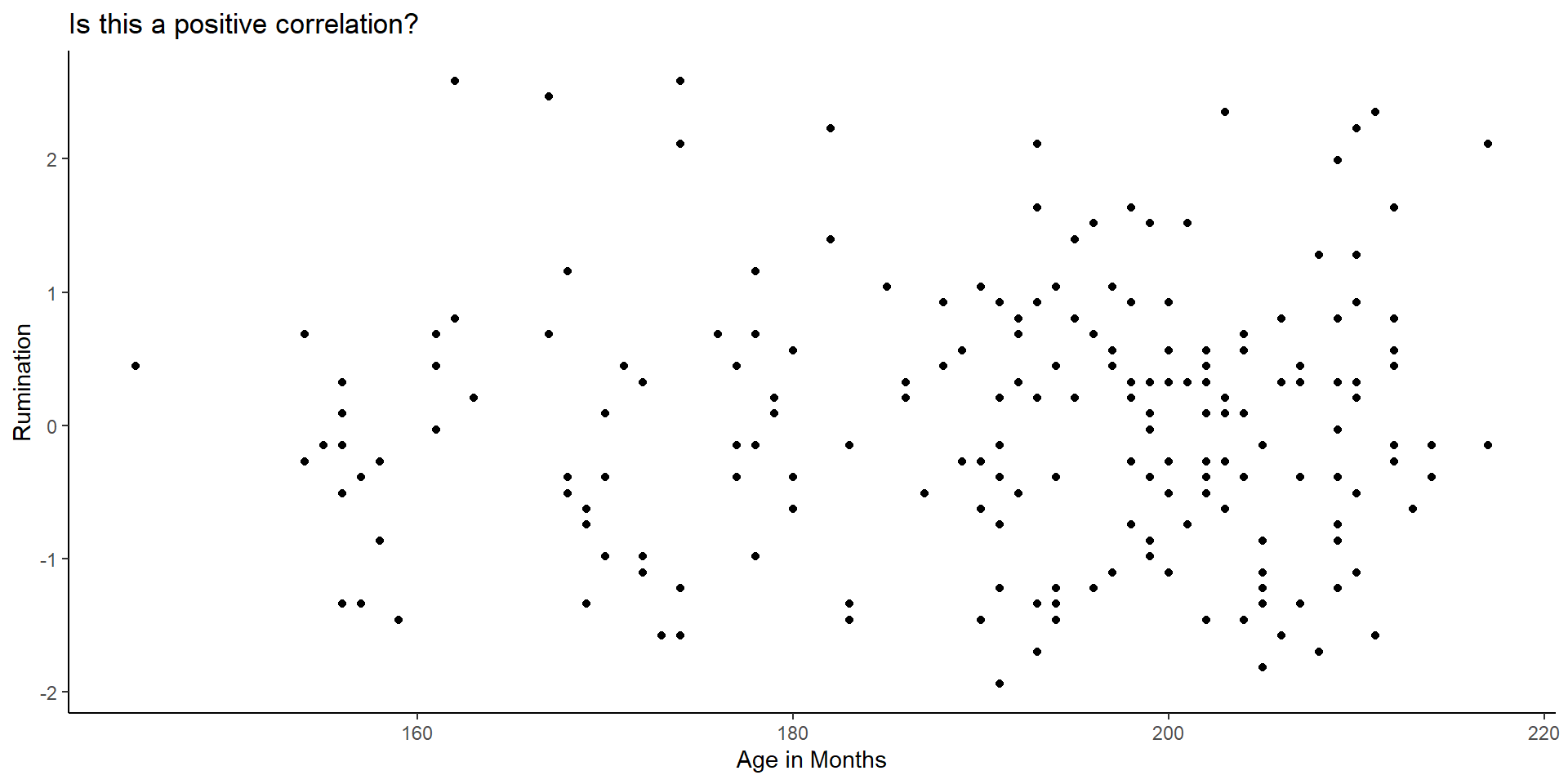
Scatter plots and direction of correlation (cont.)

Let’s add the line of linear fit:

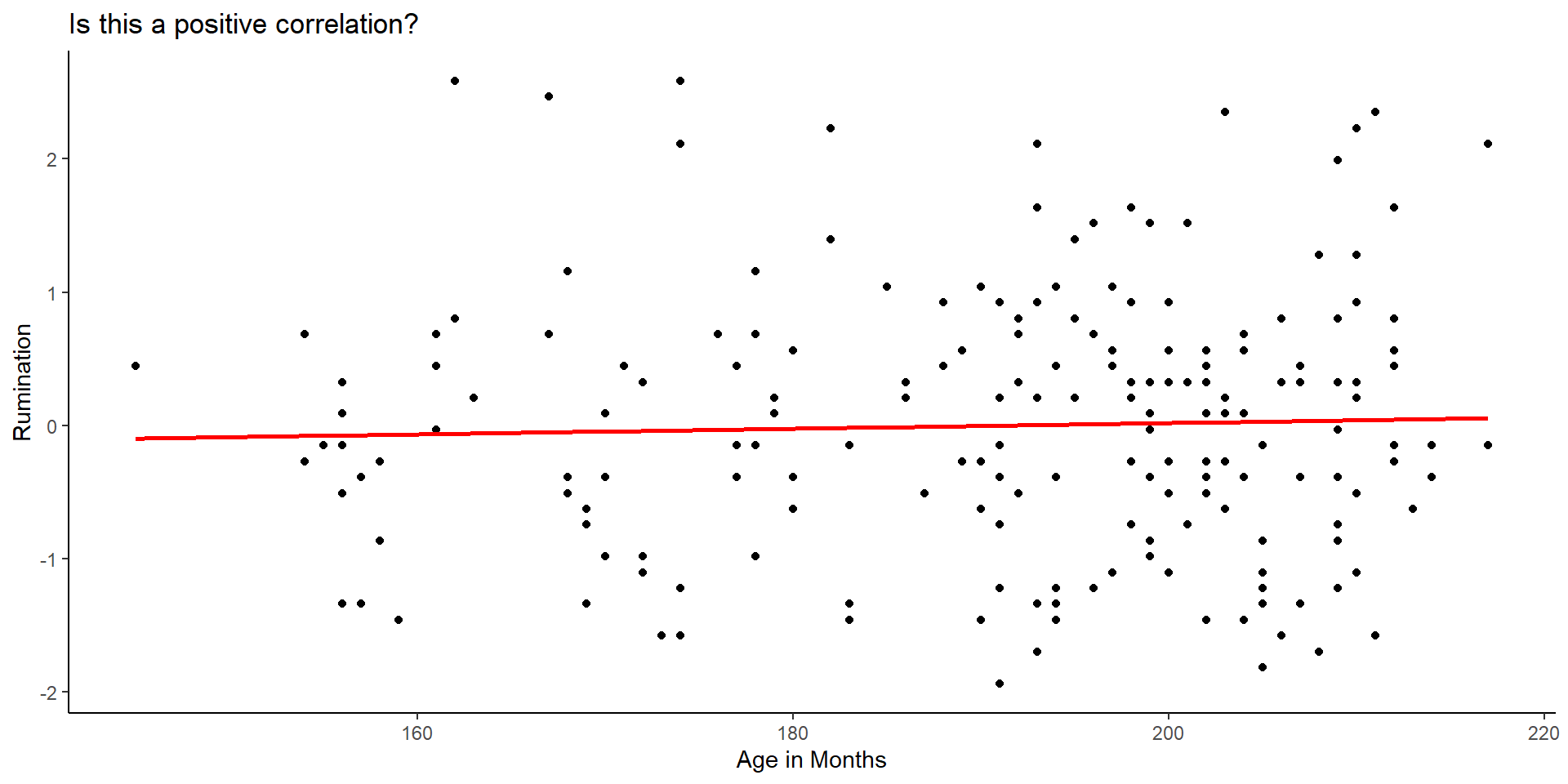
Important remarks

When the correlation is high, it means there is a large portion of shared variance between $x$ and $y$.
When the correlation is high all the values will converge towards the line of best linear fit.
When the correlation is low, the values will be sparse and far from the line of best fit.
A flat linear line means that there is not correlation between $x$ or $y$ or the correlation is remarkably low. This means $r=0$ or closer to zero.

Computer estimation time!

In R you can estimate Pearson correlations using the function cor() as showed here:

### pos is the name of the object representing my data set
cor(pos$down, pos$great)

[1] -0.359944

In this estimation, I’m calculating the correlation between the emotion DOWN and the emotion GREAT. The Pearson correlation was $r= -0.36$. Is this a strong correlation?

We could follow an ugly rule of thumb, but be careful, these are not rules cast in stone (Salkind & Shaw, 2020):

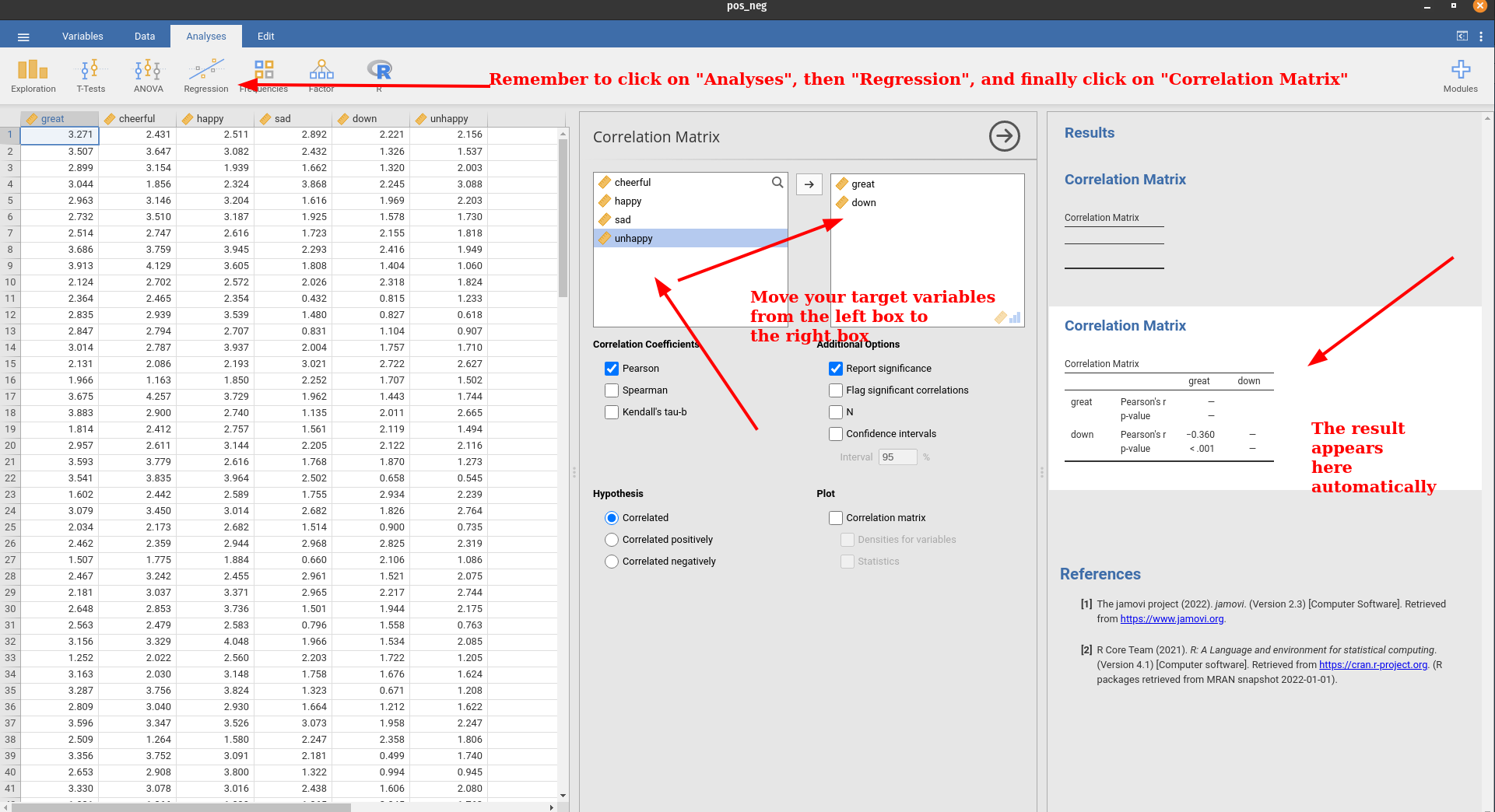
JAMOVI

References

Salkind, N. J., & Shaw, L. A. (2020). Statistics for people who (think they) hate statistics: Using r. Sage publications.