Assignment #1 – {HASO}

Description

In this assignment you’ll have to answer questions based on the presentation Introduction to Probability and Statistics and the lecture Probability distributions and random variables. Also, you may need to check the examples provided by Westfall & Henning (2013) (Chapter 1).

Please submit your answers in a Word document, Libre Office, Google document, or a pdf file rendered via Quarto. Copy the question and then answer the question in the following paragraph, similar to this example.

1) What is a parameter?

Answer: A parameter is an unknown value in a model, but it will be estimated using the data

Relevant questions related to NATURE

Please answer the following questions, if you find yourself not understanding the question please send me an email or schedule an appointment. My aim is to evaluate if I did a good job communicating the main points, in addition; I aim to evaluate if you understood the content.

Let’s imagine that you need a model relating crime rate in a “typical” city to the poverty, then you came up with the next model:

\[\begin{equation} CrimeRate = 60+5*Poverty \end{equation}\]

1.1 What kind of model is this? Provide the right term from the presentation or from page 8 in Westfall & Henning (2013). ( 10 points)

1.2 Is this model good to study crime? Answer this question based on the lecture or based on page 9 in Westfall & Henning (2013). (5 points)

In page 13, Westfall & Henning (2013) define a Purely Probabilistic Statistical Model as:

A purely probabilistic statistical model states that a variable $Y$ is produced by a pdf having unknown parameters. In symbolic shorthand, the model is given as $Y \sim p(y|\theta)$

Based on this definition, please write the name of three probability models we studied in class. (Hint: Check the lecture Probability distributions and random variables) (5 points)

We studied in class that models generate data, what is the distribution of the following model?, and what information is assumed in the “population model” or data generating process? (10 points)

## Average or mean
Mean <- 50
## Standard deviation
SD <- 20
N <- 2000

generatedValues <- rnorm(n = N, mean = Mean, sd = SD )

plot(density(generatedValues),
     xlab = "generated values",
     ylab = "p(y) or likelihood",
     main = "What is this distribution?")

I explained in class that simulations are good for learning complicated topics in statistics. I also mentioned that simulations help to explain the concept of DATA (uppercase) versus data (lowercase). Explain the concept of DATA and data using the example of tossing a coin. When we simulate one data set using the Bernoulli distribution, is this data set* DATA* or data? (10 points)
R contains data sets available for practicing. You can see the list of data sets by running data(). Run the data() function, after that select one data set, then run the function summary(). What information issummary() giving you? (5 points)

### Example: I'm running summary() with the data set named 'mtcars'. Select
### another data set from data()
data()
summary(mtcars)

In this exercise, I will introduce a new function in R. The name of this function is pipe. A pipe is a R function that helps to do several steps in one single line of code. It is like creating a chain of multiple steps.

In R, pipes are created using this sign: |>. Let’s see the following example:

library(tidyverse)
library(palmerpenguins)

  penguins |>
    filter(species == "Adelie") |>
    select(bill_depth_mm) |>
    with(mean(bill_depth_mm, na.rm = TRUE))

[1] 18.34636

In the code above, I’m performing several steps on the data set named penguins, from the package palmerpenguis. You will see the function filter() from the package dplyr. The dplyr package is already included inside the tidyverse package. The function filter() is selecting the penguins classified as “Adelie”, then I’m selecting the column “bill_depth_mm”, and finally I’m estimating the mean of “bill_depth_mm”. As you can see, you can read the pipe as “then do this”. In English you could read: filter penguins by species = “Adelie”, then select the column “bill_depth_mm”, then estimate the mean of “bill_depth_mm”.

Following this explanation, select in the life expectancy data the column “X2019”, after that estimate the mean the the column “X2019”. Include your code, and the output. (5 points)

Previuos step

To answer this question you have to install the package tidyverse, by running this code: install.packages("tidyverse", dependencies = TRUE). To use the package you have to run: library(tidyverse). You may read this information first: https://blackhill86.github.io/StatsBook/functionsPack.html . If you have already installed this package you don’t have to install it again.

You may use the following code to open the data file “lifeExpect.csv” in R:

Note

urlLife <- "https://raw.githubusercontent.com/blackhill86/mm2/refs/heads/main/dataSets/lifeExpect.csv"

lifeExpect <- read.csv(urlLife)

In class I mentioned that probability distributions are actually statistical models. They produce data, therefore they are models. I also mentioned that there is a probability model that helps to understand how counts are produced. By looking at the following probability density plot. Can you tell what is the name of this probability distribution? (5 points)

A scatter plot is useful to see the possible correlation between two continuous variables (2 points)

TRUE

FALSE

Isabel conducted a study to evaluate if there was an effect of baby formula on total fat in 1 year old babies. In this study, she had two groups, one group were babies fed with baby formula only, the other group were breast fed babies. Which option corresponds to the best model or the best models to analyze the data? (2 points)

Classical Regression Model.

t-test for paired samples.

t-test for independent samples.

Options 1 and 3 would be the best choices.

The $p$-value evaluates the magnitude of difference between two means: (2 points)

TRUE

FALSE

The effect size (Cohen’s $d$) is an standardized measure that helps to evaluate how large is the mean difference: (2 points)

TRUE

FALSE

The picture below represents a : (2 points)

Positive correlation

Negative correlation

No correlation

All the above are true

Does the following scatter plot represent a positive correlation? (2 points)

YES

The $p$-value is the probability of seeing a difference as extreme or more extreme than the difference that you observed, assuming your data come from a process where there is, in reality, no difference (Westfall & Henning, 2013) (2 points)

TRUE

FALSE

Note

Hint: Check slide #6 in the file named hypothesisTesting.html.

The following statement represents the null hypothesis: (2 points)

\[\begin{equation} H_{0}: \mu_{1} = \mu_{2} \end{equation}\]

TRUE

FALSE

When we perform hypothesis testing we collect evidence to try to reject the null-hypothesis: (2 points)

TRUE

FALSE

Constant variance is a an assumption in the Classical Regression Model: (2 points)

TRUE

FALSE

When conducting a $t$-test, you could correct your test if the variances are not equal between groups: (2 points)

TRUE

FALSE

What type of model am I estimating in the following line of code? (2 points)

lm(rumination ~ sex, data = rum)

Pearson correlation

Classical Regression Model

that’s not a statistical model in R

According the famous and ugly rule of thumb, a $p$-value less than 0.05 ($p < .05$) is considered enough evidence to claim that any estimate cannot be explained by chance alone. (2 points)

TRUE

FALSE

Before conducting a $t$-test we should check the assumption of equality of variance by performing Levene’s test: (2 points)

TRUE

FALSE

Second Part: More to do in `R`!

In this section, the aim is to practice what we have learned by estimating some models in R. If you’d like to use R, you are free to do it.

Imagine you need to evaluate the mean difference in wage. In this analysis you ask to yourself: are there differences in wage by insurance status? Estimate a model that helps you to understand the mean difference in wage when people have insurance versus people without insurance. What model will you pick?

To answer this question open the data set named wageData.csv in R. Then, conduct the appropriate statistical model. Remember that the variable wage represents the amount of dollars earn per hour. The variable health_ins is the group, factor or independent variable.

Tip

Pay attention to Lecture 7: Introduction to Hypothesis Testing

Warning

You can copy this R code to open the data set:

url <- "https://raw.githubusercontent.com/blackhill86/mm2/refs/heads/main/dataSets/wageData.csv"

wageData <- read.csv(url)

1.1 Was the value of the mean different? Are people with insurance earning more money? (5 point)

1.2 Is the mean difference explained by chance alone? How do you know? (5 points)

1.3 Create a bar plot showing the mean of wage by group (insurance vs. no insurance ). You may follow the example code below. (7 points)

Show the code

library(ggplot2)
library(dplyr)

### Estimates standard error to plot error bars

StandError <- function(x) {
 sd(x)/sqrt(length(x))
}
### Now we can estimate the mean, and SE by group,
### then we can save the information in a data frame.
summaries <- wageData |> 
  group_by(race) |>
  summarise_at("wage", list(mean= mean,
                          SE = StandError))
ggplot(summaries , aes(x=race,y = mean, fill = race)) + 
  geom_bar(position=position_dodge(), stat="identity") +
  geom_errorbar(aes(ymin=mean-SE, ymax=mean+SE), width=.1)+
  xlab("Race")+
  ylab("Estimated mean")+
  ggtitle("Example of a bar plot in R")+
  theme_classic()

In this class, I have extensively mentioned the data set rumination. We will use this data set to complete the following set of tasks.

To complete the following questions, open the data set named ruminationExam.csv in R.

Warning

You can open the dataset ruminationExam.csv in R by copying the following code:

urlRumi <- "https://raw.githubusercontent.com/blackhill86/mm2/refs/heads/main/dataSets/ruminationExam.csv"

dataRumi <- read.csv(urlRumi, na.strings = "99")

2.1. The first step is to compute a composite score for rumination and a composite score for depression. This is a very common step in psychology. You will have to add all the columns corresponding to the rumination scale and divide the total by the number of columns. The same step has to be done for the depression scale.

In the data set ruminationExam.csv the rumination scale has 13 items, the corresponding columns range from CRQS1 to CRQS13.

The depression scale has 26 items, the corresponding columns range from CDI1 to CDI26. You may follow the code below:

Show the code

library(dplyr)

dataRumi <- dataRumi|>
  mutate(depressionScore = rowMeans(pick(starts_with("CDI"))),
         rumScore = rowMeans(pick(starts_with("CR"))))

2.2. Create a scatter plot of depression by rumination. Include the figure in your answer. What do you see in the figure? Can you tell if there is a positive or negative correlation? It is a positive or negative correlation? (10 points)

2.3. Estimate a Pearson correlation between rumination and depression. Report the estimated correlation. Is this correlation explained by chance alone? (5 points)

The previous question gave you a simple example to estimate a single Pearson correlation. But, that is not realistic; many times we need to create several pairs of correlations into a matrix that we call in statistics “correlation matrix”.

In this exercise, you will need to open the data set pos_neg.csv in R. The data set pos_neg has scores that range from 1 to 5, if the person answered 5 in the great variable that means the person felt great, but if the person answered 1.8, that means that the person felt less great. You can see the data pos_neg.csv in the table below:

Warning

You can open the data set pos_neg.csv by copying this code:

urlposNeg <- "https://raw.githubusercontent.com/blackhill86/mm2/refs/heads/main/dataSets/pos_neg.csv"

pos_neg <- read.csv(urlposNeg)

3.1. Estimate a correlation matrix in R between all the emotions: great, cheerful, happy, sad, down, unhappy. Report the correlation matrix. Remember to estimate the $p$-value for all the correlations. (5 point)

Note

You may need to install the package Hmisc, then you can use the function rcorr()by running a code similar to this: rcorr(as.matrix(data), type="pearson").

3.2. Interpret your results, for example you can write something like this (10 points):

Tip

The correlation between variable 1 and variable 2 was $r = .30$ with a $p$-value $< .05$. This means that when variable 1 increases, variable 2 also increases. Whereas the correlation between variable 3 and variable 4 was negative $r = -0.38$ which means that a high score in varaible 3 is related to a low score in variable 4. Both correlations are not explained by chance alone because the $p$-value is lower than 0.05

References

Westfall, P. H., & Henning, K. S. (2013). Understanding advanced statistical methods. CRC Press Boca Raton, FL, USA:

--- title: "Assignment #1" subtitle: "120 points" title-block-banner: true author: "Esteban Montenegro-Montenegro" date: now format: html: code-tools: source: true theme: light: [sandstone, theme.scss] dark: [cyborg, theme.scss] editor: visual self-contained: true bibliography: references.bib csl: apa.csl lightbox: true --- ## Description In this assignment you'll have to answer questions based on the presentation *Introduction to Probability and Statistics* and the lecture *Probability distributions and random variables*. Also, you may need to check the examples provided by @westfall2013understanding (Chapter 1). Please submit your answers in a Word document, Libre Office, Google document, or a pdf file rendered via `Quarto`. Copy the question and then answer the question in the following paragraph, similar to this example. ::: {#example .message style="color: navy;"} *1) What is a parameter?* ::: ::: {.message style="color: navy;"} *Answer: A parameter is an unknown value in a model, but it will be estimated using the data* ::: ## Relevant questions related to NATURE Please answer the following questions, if you find yourself not understanding the question please send me an email or schedule an appointment. My aim is to evaluate if I did a good job communicating the main points, in addition; I aim to evaluate if you understood the content. 1. Let's imagine that you need a model relating crime rate in a "typical" city to the poverty, then you came up with the next model: ```{=tex} \begin{equation} CrimeRate = 60+5*Poverty \end{equation} ``` 1.1 What kind of model is this? Provide the right term from the presentation or from page 8 in @westfall2013understanding. ( 10 points) 1.2 Is this model good to study crime? Answer this question based on the lecture or based on page 9 in @westfall2013understanding. (5 points) 2. In page 13, @westfall2013understanding define a ***Purely Probabilistic Statistical Model*** as: ::: {#model .message style="color: black;"} ***A purely probabilistic statistical model states that a variable*** $Y$ is produced by a pdf having unknown parameters. In symbolic shorthand, the model is given as $Y \sim p(y|\theta)$ ::: Based on this definition, please write the name of three probability models we studied in class. (Hint: Check the lecture *Probability distributions and random variables*) (5 points) 3. We studied in class that models generate data, what is the distribution of the following model?, and what information is assumed in the "population model" or data generating process? (10 points) ```{r, echo = TRUE} ## Average or mean Mean <- 50 ## Standard deviation SD <- 20 N <- 2000 generatedValues <- rnorm(n = N, mean = Mean, sd = SD ) plot(density(generatedValues), xlab = "generated values", ylab = "p(y) or likelihood", main = "What is this distribution?") ``` 4. I explained in class that simulations are good for learning complicated topics in statistics. I also mentioned that simulations help to explain the concept of DATA (uppercase) versus data (lowercase). Explain the concept of ***DATA*** and ***data*** using the example of tossing a coin. When we simulate one data set using the Bernoulli distribution, is this data set\* **DATA**\* or ***data***? (10 points) 5. `R` contains data sets available for practicing. You can see the list of data sets by running `data()`. Run the `data()` function, after that select one data set, then run the function `summary()`. What information is`summary()` giving you? (5 points) ```{r, eval=FALSE} ### Example: I'm running summary() with the data set named 'mtcars'. Select ### another data set from data() data() summary(mtcars) ``` 6. In this exercise, I will introduce a new function in `R`. The name of this function is ***pipe***. A pipe is a `R` function that helps to do several steps in one single line of code. It is like creating a chain of multiple steps. In `R`, pipes are created using this sign: `|>`. Let's see the following example: ```{r, message=FALSE} library(tidyverse) library(palmerpenguins) penguins |> filter(species == "Adelie") |> select(bill_depth_mm) |> with(mean(bill_depth_mm, na.rm = TRUE)) ``` In the code above, I'm performing several steps on the data set named `penguins`, from the package `palmerpenguis`. You will see the function `filter()` from the package `dplyr`. The `dplyr` package is already included inside the `tidyverse` package. The function `filter()` is selecting the penguins classified as "Adelie", then I'm selecting the column "bill_depth_mm", and finally I'm estimating the mean of "bill_depth_mm". As you can see, you can read the pipe as "then do this". In English you could read: filter penguins by species = "Adelie", then select the column "bill_depth_mm", then estimate the mean of "bill_depth_mm". Following this explanation, select in the life expectancy data the column "X2019", after that estimate the mean the the column "X2019". Include your code, and the output. (5 points) ::: callout-important ### Previuos step To answer this question you have to install the package `tidyverse`, by running this code: `install.packages("tidyverse", dependencies = TRUE)`. To use the package you have to run: `library(tidyverse)`. You may read this information first: <https://blackhill86.github.io/StatsBook/functionsPack.html> . If you have already installed this package you don't have to install it again. ::: You may use the following code to open the data file "lifeExpect.csv" in `R`: ::: callout-note ```{r} urlLife <- "https://raw.githubusercontent.com/blackhill86/mm2/refs/heads/main/dataSets/lifeExpect.csv" lifeExpect <- read.csv(urlLife) ``` ::: 7. In class I mentioned that probability distributions are actually statistical models. They produce data, therefore they are models. I also mentioned that there is a probability model that helps to understand how counts are produced. By looking at the following **probability density plot**. Can you tell what is the name of this probability distribution? (5 points) ```{r, include=TRUE, echo=FALSE, message=FALSE, warning=FALSE} set.seed(2364) library("VGAM") plot(density(rzipois(100, lambda = 9, pstr0 = 0.5), kernel = "gaussian", bw = 0.5),main="Probability Density Plot", xlab="Number of times I say \"right\" in class for a semester", ylab="Likelihood" ) ```  8. A scatter plot is useful to see the possible correlation between two continuous variables (2 points) {{< fa circle-notch >}} TRUE {{< fa circle-notch >}} FALSE ------------------------------------------------------------------------ 09. Isabel conducted a study to evaluate if there was an effect of baby formula on total fat in 1 year old babies. In this study, she had two groups, one group were babies fed with baby formula only, the other group were breast fed babies. Which option corresponds to the best model or the best models to analyze the data? (2 points) {{< fa circle-notch >}} Classical Regression Model. {{< fa circle-notch >}} t-test for paired samples. {{< fa circle-notch >}} t-test for independent samples. {{< fa circle-notch >}} Options 1 and 3 would be the best choices. ------------------------------------------------------------------------ 10. The $p$-value evaluates the magnitude of difference between two means: (2 points) {{< fa circle-notch >}} TRUE {{< fa circle-notch >}} FALSE ------------------------------------------------------------------------ 11. The effect size (Cohen's $d$) is an standardized measure that helps to evaluate how large is the mean difference: (2 points) {{< fa circle-notch >}} TRUE {{< fa circle-notch >}} FALSE ------------------------------------------------------------------------ 12. The picture below represents a : (2 points)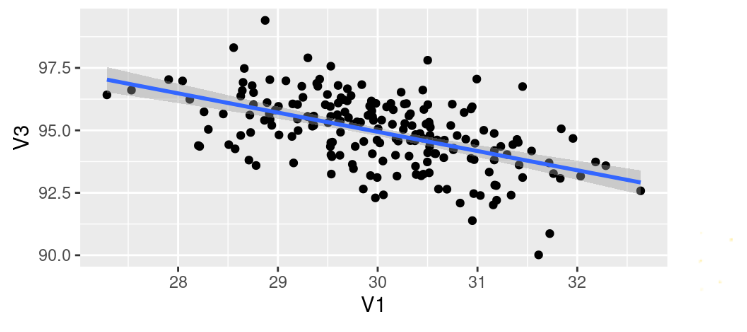 ![](corre1.png) {{< fa circle-notch >}} Positive correlation {{< fa circle-notch >}} Negative correlation {{< fa circle-notch >}} No correlation {{< fa circle-notch >}} All the above are true ------------------------------------------------------------------------ 13. Does the following scatter plot represent a positive correlation? (2 points) {{< fa circle-notch >}} YES {{< fa circle-notch >}} NO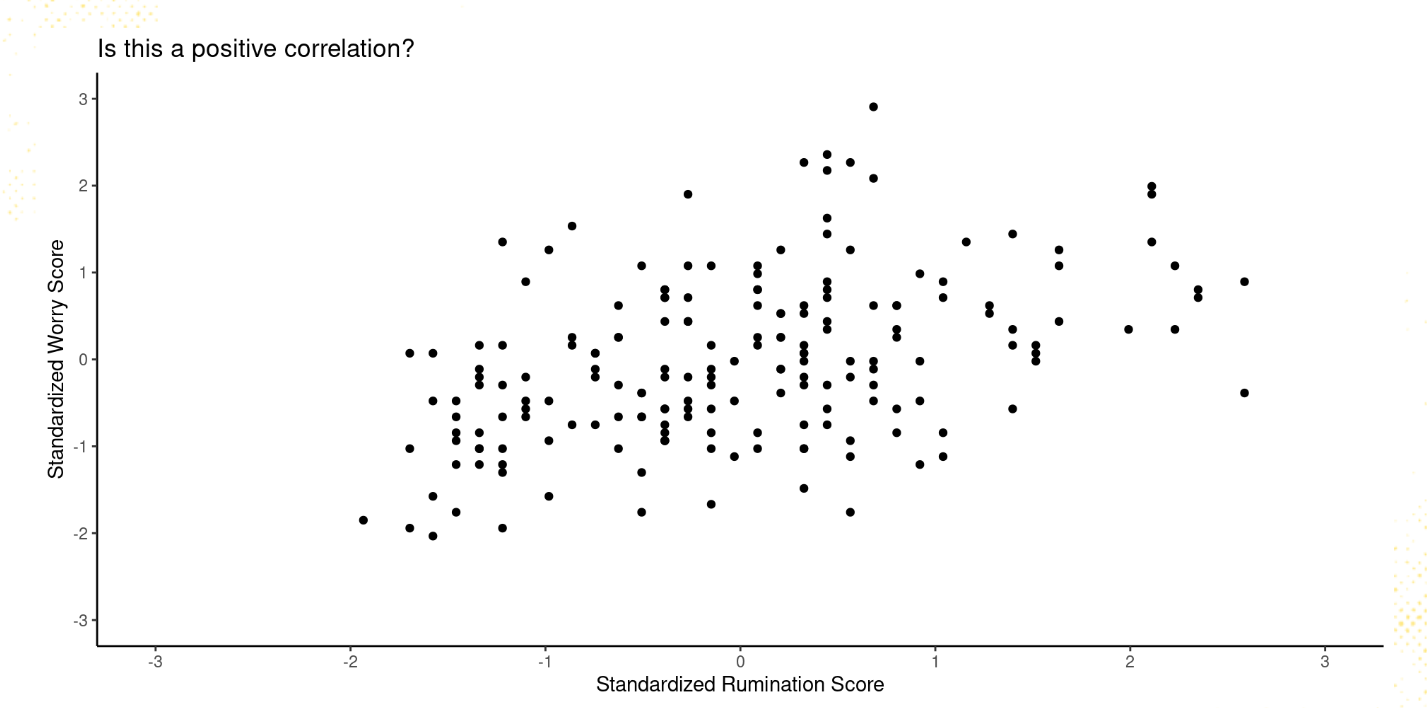 ![](corre2.png) ------------------------------------------------------------------------ 14. The $p$-value is the probability of seeing a difference as extreme or more extreme than the difference that you observed, assuming your data come from a process where there is, in reality, no difference [@westfall2013understanding] (2 points) {{< fa circle-notch >}} TRUE {{< fa circle-notch >}} FALSE ::: callout-note Hint: Check slide #6 in the file named `hypothesisTesting.html`. ::: ------------------------------------------------------------------------ 15. The following statement represents the null hypothesis: (2 points) ```{=tex} \begin{equation} H_{0}: \mu_{1} = \mu_{2} \end{equation} ``` {{< fa circle-notch >}} TRUE {{< fa circle-notch >}} FALSE ------------------------------------------------------------------------ 16. When we perform hypothesis testing we collect evidence to try to reject the null-hypothesis: (2 points) {{< fa circle-notch >}} TRUE {{< fa circle-notch >}} FALSE ------------------------------------------------------------------------ 17. Constant variance is a an assumption in the Classical Regression Model: (2 points) {{< fa circle-notch >}} TRUE {{< fa circle-notch >}} FALSE ------------------------------------------------------------------------ 18. When conducting a $t$-test, you could correct your test if the variances are not equal between groups: (2 points) {{< fa circle-notch >}} TRUE {{< fa circle-notch >}} FALSE ------------------------------------------------------------------------ 19. What type of model am I estimating in the following line of code? (2 points) ```{r, echo=TRUE,eval=FALSE} lm(rumination ~ sex, data = rum) ``` {{< fa circle-notch >}} Pearson correlation {{< fa circle-notch >}} Classical Regression Model {{< fa circle-notch >}} that's not a statistical model in R ------------------------------------------------------------------------ 20. According the famous and ugly rule of thumb, a $p$-value less than 0.05 ($p < .05$) is considered enough evidence to claim that any estimate cannot be explained by chance alone. (2 points) {{< fa circle-notch >}} TRUE {{< fa circle-notch >}} FALSE 21. Before conducting a $t$-test we should check the assumption of equality of variance by performing Levene's test: (2 points) {{< fa circle-notch >}} TRUE {{< fa circle-notch >}} FALSE ## Second Part: More to do in `R`! In this section, the aim is to practice what we have learned by estimating some models in `R`. If you'd like to use `R`, you are free to do it. 1. **Imagine you need to evaluate the mean difference in wage. In this analysis you ask to yourself: are there differences in wage by insurance status? Estimate a model that helps you to understand the mean difference in wage when people have insurance versus people without insurance. What model will you pick?** To answer this question open the data set named `wageData.csv` in `R`. Then, conduct the appropriate statistical model. Remember that the variable `wage` represents the amount of dollars earn per hour. The variable `health_ins` is the group, factor or independent variable. ::: callout-tip Pay attention to [Lecture 7: Introduction to Hypothesis Testing](https://m-square.net/lecture7/hypothesisTesting.html#lecture7){target="_blank"} ::: ::: callout-warning You can copy this `R` code to open the data set: ```{r} url <- "https://raw.githubusercontent.com/blackhill86/mm2/refs/heads/main/dataSets/wageData.csv" wageData <- read.csv(url) ``` ::: 1.1 Was the value of the mean different? Are people with insurance earning more money? (5 point) 1.2 Is the mean difference explained by chance alone? How do you know? (5 points) 1.3 Create a bar plot showing the mean of wage by group (insurance vs. no insurance ). You may follow the example code below. (7 points) ```{r} #| code-fold: true #| code-summary: "Show the code" library(ggplot2) library(dplyr) ### Estimates standard error to plot error bars StandError <- function(x) { sd(x)/sqrt(length(x)) } ### Now we can estimate the mean, and SE by group, ### then we can save the information in a data frame. summaries <- wageData |> group_by(race) |> summarise_at("wage", list(mean= mean, SE = StandError)) ggplot(summaries , aes(x=race,y = mean, fill = race)) + geom_bar(position=position_dodge(), stat="identity") + geom_errorbar(aes(ymin=mean-SE, ymax=mean+SE), width=.1)+ xlab("Race")+ ylab("Estimated mean")+ ggtitle("Example of a bar plot in R")+ theme_classic() ``` 2. **In this class, I have extensively mentioned the data set `rumination`. We will use this data set to complete the following set of tasks.** To complete the following questions, open the data set named `ruminationExam.csv` in `R`. ::: callout-warning You can open the dataset `ruminationExam.csv` in `R` by copying the following code: ```{r} urlRumi <- "https://raw.githubusercontent.com/blackhill86/mm2/refs/heads/main/dataSets/ruminationExam.csv" dataRumi <- read.csv(urlRumi, na.strings = "99") ``` ::: 2.1. The first step is to compute a composite score for rumination and a composite score for depression. This is a very common step in psychology. You will have to add all the columns corresponding to the rumination scale and divide the total by the number of columns. The same step has to be done for the depression scale. In the data set `ruminationExam.csv` the rumination scale has 13 items, the corresponding columns range from `CRQS1` to `CRQS13`. The depression scale has 26 items, the corresponding columns range from `CDI1` to `CDI26`. You may follow the code below: ```{r} #| code-fold: true #| code-summary: "Show the code" library(dplyr) dataRumi <- dataRumi|> mutate(depressionScore = rowMeans(pick(starts_with("CDI"))), rumScore = rowMeans(pick(starts_with("CR")))) ``` 2.2. Create a scatter plot of depression by rumination. Include the figure in your answer. What do you see in the figure? Can you tell if there is a positive or negative correlation? It is a positive or negative correlation? (10 points) 2.3. Estimate a Pearson correlation between rumination and depression. Report the estimated correlation. Is this correlation explained by chance alone? (5 points) 3. **The previous question gave you a simple example to estimate a single Pearson correlation. But, that is not realistic; many times we need to create several pairs of correlations into a matrix that we call in statistics "correlation matrix".** In this exercise, you will need to open the data set `pos_neg.csv` in `R`. The data set `pos_neg` has scores that range from 1 to 5, if the person answered 5 in the `great` variable that means the person felt `great`, but if the person answered 1.8, that means that the person felt less `great`. You can see the data `pos_neg.csv` in the table below: ::: callout-warning You can open the data set `pos_neg.csv` by copying this code: ```{r} urlposNeg <- "https://raw.githubusercontent.com/blackhill86/mm2/refs/heads/main/dataSets/pos_neg.csv" pos_neg <- read.csv(urlposNeg) ``` ::: ```{r, message=FALSE, error=FALSE} #| echo: false library(DT) dat1 <- read.csv("pos_neg.csv") datatable(dat1, class = 'cell-border stripe', caption = "Positive and Negative Affect Data Set") ``` 3.1. Estimate a correlation matrix in `R` between all the emotions: great, cheerful, happy, sad, down, unhappy. **Report the correlation matrix**. Remember to estimate the $p$-value for all the correlations. (5 point) ::: callout-note You may need to install the package `Hmisc`, then you can use the function `rcorr()`by running a code similar to this: `rcorr(as.matrix(data), type="pearson")`. ::: 3.2. Interpret your results, for example you can write something like this (10 points): ::: callout-tip *The correlation between `variable 1` and `variable 2` was* $r = .30$ with a $p$-value $< .05$. This means that when `variable 1` increases, `variable 2` also increases. Whereas the correlation between `variable 3` and `variable 4` was negative $r = -0.38$ which means that a high score in `varaible 3` is related to a low score in `variable 4`. Both correlations are not explained by chance alone because the $p$-value is lower than 0.05 :::

Description

Relevant questions related to NATURE

Second Part: More to do in R!

References

Second Part: More to do in `R`!