Assignment #2

400 points

Author

Esteban Montenegro-Montenegro

Published

October 30, 2024

Description

In this second assignment, you’ll have to solve several applied tasks. You’ll have the chance to solve applied data analysis tasks using R, or Jamovi.

What happens if you don’t understand how to answer an exercise ?

In this assigment I will provide videos on how to solve the exercises, or I’ll explain the solution in class. If after the explanation, you still have questions don’t hesitate to send me an email.

Part 1: Review important concepts

In this section, you will see TRUE/FALSE questions, or multiple choice questions. Select only one option. (10 points each correct answer).

Please copy the question along with your answer in a Word document.

  1. A \(t\)-test may be used when my dependent variable is continuous and the independent variable is a nominal variable with only two levels:


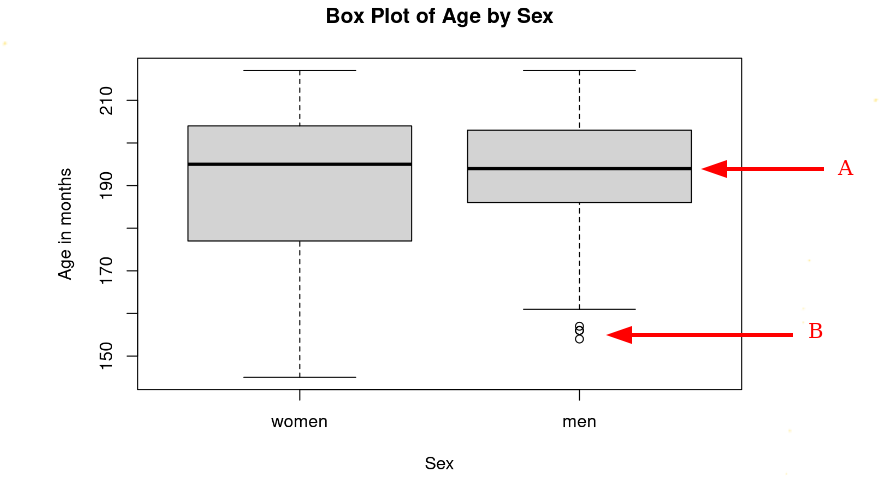
  1. The options to label A and B are: (check the module "Data Visualizations on Canvas")



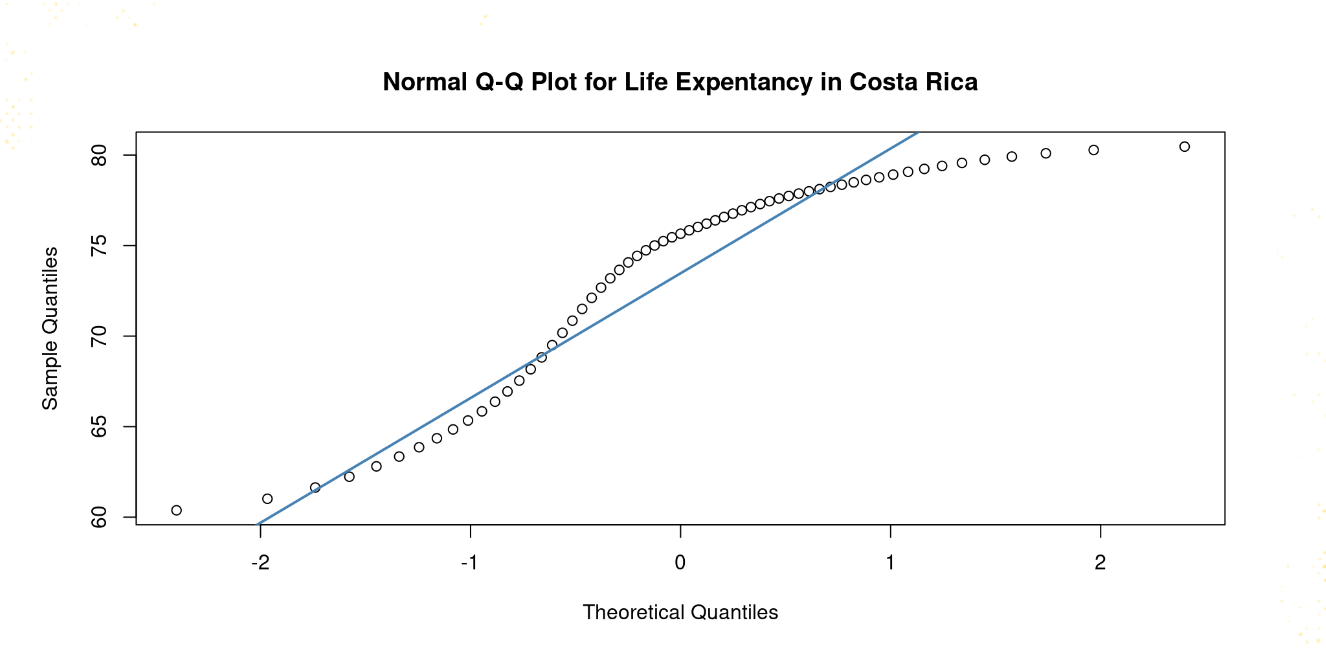
  1. The above figure is a QQ-plot, can you conclude that Life Expectancy in Costa Rica comes from a normally distributed process? (check the module "Data Visualizations on Canvas")


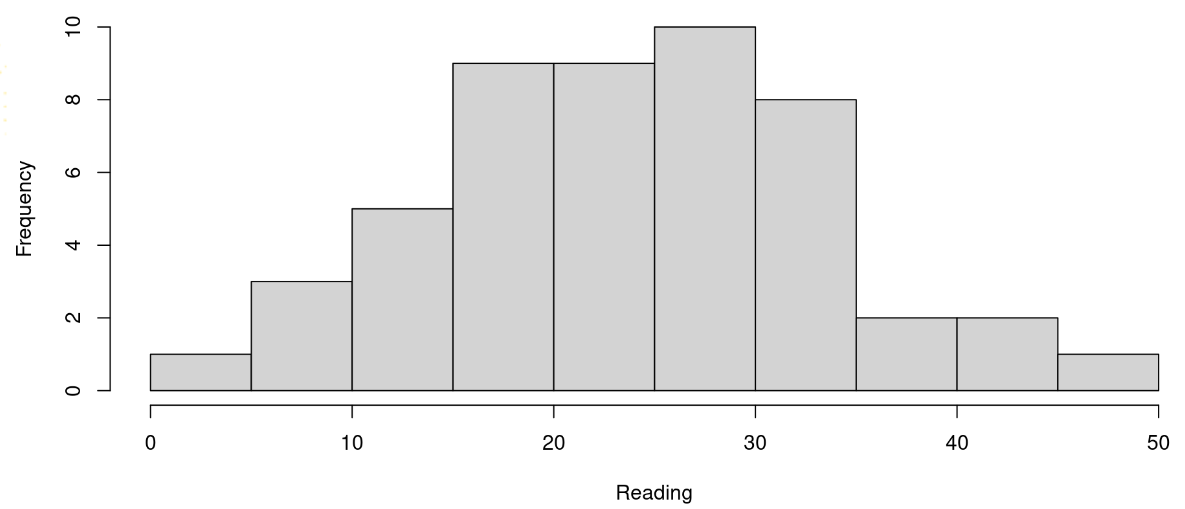
  1. The above figure represents a:




  1. In the Classical Regression Model, the estimated slope of the regression is often represented with the Greek letter \(\beta\) (beta). Taking this into consideration, if my estimated \(\beta\) is equals to a value greater than \(0\), I can conclude that there is a positive relationship between my outcome and my predictor:


  1. The Classical Regression Model does not have any distributional assumption on the predictors


  1. The Classical Regression Model assumes that the dependent variable or outcome must come from a normal distribution:


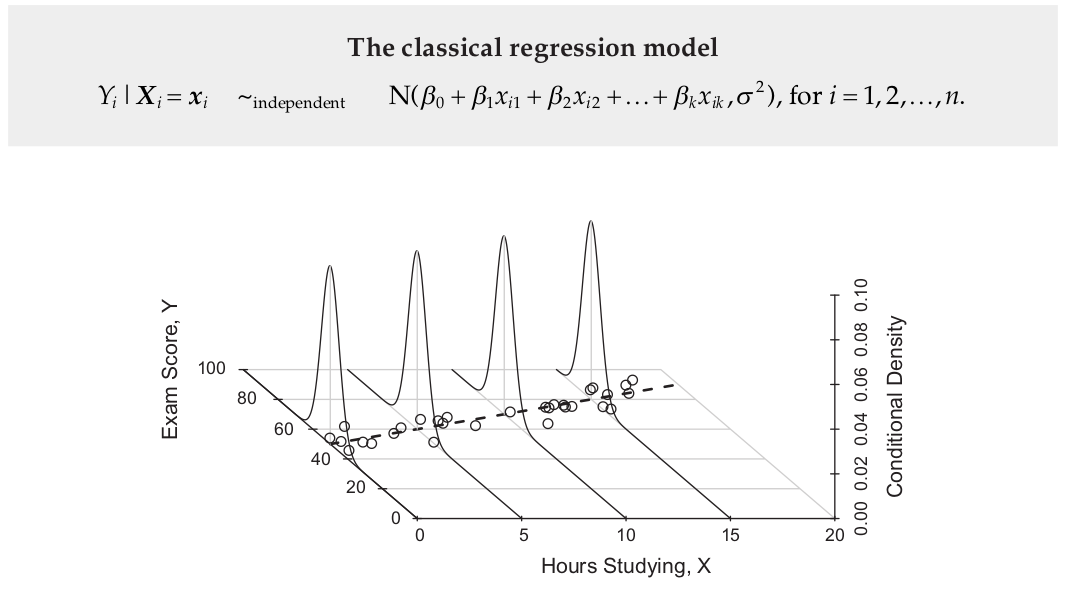
  1. The following model represents:
\[\begin{equation} Y = \beta_{0}+ \beta_{1}X_{1} + \beta_{2}X_{2} + \epsilon \end{equation}\]



  1. One of the assumptions of ANOVA is constant variance in all groups:


  1. Pedro performed an experiment aiming to delay dementia symptoms in older adults. In this study, Pedro created three random conditions: A) A group attending yoga class, B) A group attending weight lifting, and finally, C) A group attending nutrition classes. Pedro measured the working memory capacity at the end of the study as a dependent variable. The problem for Pedro is that he doesn’t know which statistical model he should estimate.

What model should Pedro estimate on his data to test the mean differences between groups?





  1. According to the figure above, the Classical Regression Model assumes that the conditional probability distribution functions \(p(y|x)\) (y given x) are normal distributions:



  1. Again, following the figure above, we can say that the dashed line represents the linearity assumption:



  1. We can include nominal variables as predictors in a Classical Regression Model, but first we need to create dummy coded variables:


  1. The Classical Regression Model requires a continuous dependent variable:


  1. In the following figure \(\beta_{0}\) is called the “intercept”, and it represents the vertical height or distance from zero in \(Y\):


  1. The following table represents:






Second Part: Short answer questions

In this section, I expect short answers, where you explain in your own words relevant concepts:

  1. Explain in your own words how to transform a nominal variable into several dummy coded variables. You may provide an example to make your explanation easier to follow. (10 points)

  2. Describe the assumptions of the Classical Regression Model, you may check the lecture Correlation and Regression Models Part 2. (10 points)

Third Part: Playing with JAMOVI and/or R

In this part you will use JAMOVI or R to answer several questions, the questions are a guide into different steps when performing an ANOVA.

JAMOVI users

You will use the data file named anovaData.csv, you may download the file from here. You will not use this link if you are planning on solving this part with R.

R users

You will need the following code to open the data set in R:

url <- "https://raw.githubusercontent.com/blackhill86/mm2/refs/heads/main/dataSets/anovaData.csv"

interData <- read.csv(url)

The data for this exercise is real data from an experimental intervention performed in Costa Rica in 2011. In this study, we aimed to answer the following question:

Will an intervention focused on improving autobiographical memory delay dementia symptoms?

Based on this question, we design an experiment where we assigned aging adults to 4 different conditions:

  • Condition A: Participants with mild cognitive impairment received the intervention.

  • Condition B: Participants with mild cognitive impairment did not receive the intervention.

  • Condition C: Healthy participants without cognitive impairment received the treatment.

  • Condition D: Healthy participants without cognitive impairment did not receive the treatment.

We measured the cognitive performance of the participants as dependent variable. The cognitive performance was measured before the intervention started, and it was measured again once the intervention finished. We utilized the Cambridge Cognition Examination (CAMCOG) to determine their cognitive performance. This is a long battery of tests, and at the end you can compute a total score that represents the cognitive status.

Higher scores in the CAMCOG are evidence of better cognitive performance, while lower scores represent a low cognitive performance.

After this explanation I hope the content of the data is startarting to make sense. In the data set anovaData.csv you will find the following columns:

  • ID: The study identification number for each participant.

  • CAMCOG_pre: the total score before the intervention started.

  • CAMCOG_post: the total score after the intervention finished.

  • Group: The intervention group where:

    • A: Participants with mild cognitive impairment received the intervention.
    • B: Participants with mild cognitive impairment did not receive the intervention.
    • C: Healthy participants without cognitive impairment received the treatment.
    • D: Healthy participants without cognitive impairment did not receive the treatment.
Video

You may watch this video to solve this part using JAMOVI.

  1. Report the means and standard deviations of the CAMCOG_post by Group, paste the table from JAMOVI or R. In addition, create a plot in JAMOVI or R showing the mean values of CAMCOG_post by Group. (40 points)

  2. Interpret the estimated mean values. Do you see a large difference in the mean score when comparing healthy aging adults versus aging adults with dementia? Do you observe in the bar plot a remarkable difference between groups A and B? ( 10 points)

  3. ANOVA has two important assumptions, constant variance and normality. Perform the Shapiro-Wilk’s test, to asses the normality assumption, and the Levene’s test to evaluate the assumption of constant variance. Paste the tables from JAMOVI or R and interpret the results. (20 points).

  4. Perform an omnibus ANOVA analysis to determine if there is any mean difference not explained by chance alone. Paste the table from JAMOVI or R in your answer (20 points).

  5. According to the \(p\)-value. What is your conclusion? (10 point)

  6. At this point we have performed a omnibus test, this test does not tell which group differs beyond chance from the other groups. Perform a post-hoc analysis to determine where are the differences between groups and which differences are not explained by chance alone. Paste the table generated in JAMOVI. After that, interpret the results. (20 points)

Standard Error and confidence intervals

In class I briefly explained two important concepts in frequentist statistics: the standard error, and confidence intervals.

If you don’t remember I will do a refresher in the next lines.

Standard Error

You may remember that we always work with data (lowercase), therefore our estimates could be far from Data. For example, if I ask to the class: How many romantic partners have you had in your life? I might get a mean of 3.3 romantic partners. Is this mean close or far from the true mean in Nature?

To answer this question we can calculate something called standard error. All estimates can have a standard error. When you estimate a mean you could estimate a standard error, or when you estimate the slope of a regression model, you can calculate the standard error of your estimate. The standard error will tell you how far are your from the TRUE estimate in Nature.

Question 7 (20 points)
  1. In the next chunk of code, I’m generating data from the Gaussian distribution. N represents the number of observations or hypothetical sample size, the letter M represents the TRUE mean, and SD is the value for the TRUE standard deviation. The object named standardError contains the standard error of the mean. Change the value for N, write a large number instead of number 10. What happened to the estimated standard error of the mean?

Confidence intervals

The confidence intervals will help you to measure how close you are to the TRUE value in Nature. Every estimate you calculate will have a confidence interval. A confidence interval is a set of two values, one value is the lower bound of the interval and the other is the lower bound of the interval.

The standard error and the confidence intervals are related, you can see the estimation of the mean’s confidence interval:

\[\begin{equation} \bar{x} \pm 1.96 \frac{\hat{\sigma}}{ \sqrt{n}} \end{equation}\]

Where,

\(\bar{x}\) is the estimated mean.
\(\hat{\sigma}\) is the estimated standard deviation.
\(1.96\) is the 97.5 percentile in the standard normal distribution (Gaussian).

The term \(\frac{\hat{\sigma}}{ \sqrt{n}}\) is the standard error multiplied by \(+1.96\) and \(-1.96\).This estimation will get you a 95% confidence interval.

Example time

In this example, I’m estimating a regression model where the score of a cognitive test call Trail Making is predicted by Oxygen uptake efficiency slope (OUES). This means, I am testing if the maximum level of oxygen is related to performance in a cognitive test.

You will see in the output a column named 95% CI, that column has two sets of confidence intervals. The intercept has confidence intervals corresponding to \([18.99, 37.02]\), and the confidence intervals corresponding to the slope of OUES are \([-3.29, 45.35]\).

These are the intervals where the TRUE value is located based on our estimated model. In other words, we are 95% confident that the TRUE value for the OUES slope is a number between -3.29 and 45.35.

But, there is something bad with this model. The confidence intervals are very wide, we need a model that provides narrower confidence intervals, or we need to collect more data. More observations would decrease the uncertainty in the estimation.

library(parameters)

url <- "https://raw.githubusercontent.com/blackhill86/mm2/refs/heads/main/dataSets/ouesData.csv"

ouesData <- read.csv(url)

fitOues <- lm(Trail_A ~ OUES2 , data = ouesData)

model_parameters(fitOues)
Parameter   | Coefficient |    SE |         95% CI | t(136) |      p
--------------------------------------------------------------------
(Intercept) |       28.00 |  4.56 | [18.99, 37.02] |   6.14 | < .001
OUES2       |       21.03 | 12.30 | [-3.29, 45.35] |   1.71 | 0.090 

Uncertainty intervals (equal-tailed) and p-values (two-tailed) computed
  using a Wald t-distribution approximation.
Question 8 (20 points)
  1. The next exercise might be useful to understand how to understand the confidence intervals. In the code below, I’m using the following model to generate one data set with 10 observations:

\[Y \sim 1 + (0.2)X_{1} + (0.3)X_{2} + (0.4)X_{2} + \epsilon \tag{1}\]

After generating the data, I’m estimating the model. However, the confidence intervals are very wide and the standard error is large. How can we make the confidence intervals narrower? Once you know the answer modify the code accordingly.

Model selection

We recently studied basics on Model Selection. This is a relevant topic in statistics, because afterall our job is find the model that best fits the data.

In the next set of questions you will get access to the data set named ouesData.csv. If you are planning on answering this question using JAMOVI you will need to download the data set from this link CLICK HERE

If you are using R you will need the following code to open the ouesData in your R session:

library(parameters)

url <- "https://raw.githubusercontent.com/blackhill86/mm2/refs/heads/main/dataSets/ouesData.csv"

ouesData <- read.csv(url)

What is the story behind the the data set ouesData?

As you might imagine, you will need to read a story about this data set. This was a project conducted by several researchers from Costa Rica and United States.

This is a meme, the character is Abraham from The Simpsons saying: When I was young I destroyed several research projects. But no worries, I can do worse

The aim was to collect information to understand why Costaricans have a longer life compare to most people in United States. I was part of the team, I helped collecting some variables, and at the end I had a humble role as a data analyst.

This ouesData is only a small portion of variables collected in the context of the project named Epidemiology and Development of Alzheimer’s Disease (EDAD). All participants are aging adults older than 60 years old.

The variables included in this data set are:

Stroop_color: The first part of the Stroop test.

Trail_A,Trail_A_errors, Trail_B, Trail_B_errors: Trail Making Test

OUES: Oxygen uptake efficiency slope

VO2peak: Oxygen capacity

WAISR_block: WAIS block design.

WAISR_DSS: Digit Symbol Substitution Test

Six_min_walk: Distance walked in yards. Not useful for model selection.

HR_max: Maximum heart rate during the 6 minutes walk.

HR_pre: Heart rate before the 6 minutes walk.

Female: gender, 1= Female, 0 = Male.

delayedLM: delayed logic memory.

SRT_free_recall_trial1, SRT_free_recall_trial2, and SRT_free_recall_trial3: Buschke Selective Reminding Test (SRT) is when a participant is asked to recall as many words as possible from a list of words without a cue.

logicMemory: logic memory, how much detail can the participant remember after hearing a story.

fatTotal: Total body fat.

Country: 1= Kansas, 0= Costa Rica.

BMI: Body Mass Index.

SRT_total: Total score for the Buschke Selective Reminding Test (SRT).

Question 9 (60 points)
  1. After reading about the variables included in the ouesData. Estimate a linear regression, and select the best model based on the AIC value as shown in class. You may consult the presentation on this link CLICK HERE

You may select the outcome and the predictors from this list:

  • Stroop_color
  • Trail_A
  • Trail_B
  • OUES
  • VO2peak
  • WAISR_block
  • WAISR_DSS
  • HR_max
  • HR_pre
  • Age
  • Female
  • delayedLM
  • logicMemory
  • fatTotal
  • BMI
  • Country
  • SRT_total

You will need to modify the following code if you are answering this question using R:

library(MASS)
library(tidyverse)
### Omit missing values

ouesDataNoMissing <- ouesData |>
  dplyr::select(OUES,
VO2peak,
 WAISR_block,
 WAISR_DSS,
 HR_max) |>
 drop_na()

### Estimates the null model or the worse model
interceptModel <- lm(WAISR_block ~ 1, 
                     data = ouesDataNoMissing )

### This will help you to select the best model automatically.
modelSelection <- stepAIC(interceptModel,
                          scope = list(upper = ~OUES + VO2peak + WAISR_DSS + HR_max, 
                                       lower = ~1), 
                          direction = "both",
                          trace = FALSE)

model_parameters(modelSelection)
Parameter   | Coefficient |   SE |        95% CI | t(129) |      p
------------------------------------------------------------------
(Intercept) |       13.70 | 3.84 | [6.10, 21.30] |   3.57 | < .001
WAISR DSS   |        0.41 | 0.08 | [0.24,  0.58] |   4.86 | < .001

Uncertainty intervals (equal-tailed) and p-values (two-tailed) computed
  using a Wald t-distribution approximation.