Code
## Link to the data set:
dataLink <-"https://raw.githubusercontent.com/blackhill86/mm2/refs/heads/main/dataSets/anovaData.csv"
autoMemory <- read.csv(dataLink) 240 points
Esteban Montenegro-Montenegro
December 2, 2024
In this “exam” you will need to answer several theoretical questions, plus R activities. Some of the hands on questions can be answered in Jamovi but, it will take you more time to answer them using Jamovi. As always, this is just another excuse for adding another lecture, my goal is that you are exposed to new topics and statiscal models that are useful in psychology. You may work in pairs this time and submit one single file for each team.
HINT: Check Lecture 1) (10 points)In my extra fun lectures, I got so excited teaching and I forgot to talk more about repeated measures, and how can we analyze longitudinal data. In the examples that I’ll provide we’ll analyze only two measurements points. There are other models to deal with multiple measures such as your heart rate measured every second by your smart watch, or the changes in working memory by month in toddlers; I will not cover details about these models, but I’ll try to introduce some basics.
I will start from the simpliest case, the famous \(t\)-test for repeated measures.
Consider research designs where you evaluate your participants before an intervention, and then you evaluate them again after the intervention.
For example, you could develop an intervantion to help your participants to stop smoking tobacco. You could measure how many cigarettes they smoked before then intervention, and asked again how many cigarettes are they consuming per day after the intervention.
You may remember the data set anovaData. This data set was the product of an intervention to reduce the dementia symptons in a group of older adults in Costa Rica. You may remember that the outcome variable is the score in the total score in the CAMCOG test. The first time we analyze this data we only tested a one-way ANOVA on the post test. I didn’t mention we measured the cognitive performance before the intervention.
In this case we can ask the following question:
Are the CAMCOG scores before the intervantion different from the CAMCOG scores after the intervantion?
We can try to answer this question estimating a repeated measures t-test.
First let’s take a look at the data so you can remember the variables in the data set.
| ID | CAMCOG_post | CAMCOG_pre | Group |
|---|---|---|---|
| 1 | 80.72587 | 36.62587 | A |
| 2 | 83.84728 | 32.59728 | A |
| 3 | 127.88547 | 35.58547 | A |
| 4 | 135.97629 | 41.67629 | A |
| 5 | 86.70662 | 42.60662 | A |
| 6 | 81.97158 | 30.72158 | A |
| 7 | 131.40294 | 39.10294 | A |
| 8 | 127.77319 | 33.47319 | A |
| 9 | 80.77016 | 36.67016 | A |
| 10 | 87.50895 | 36.25895 | A |
| 11 | 125.89154 | 49.11154 | B |
| 12 | 125.77103 | 46.99103 | B |
| 13 | 72.35793 | 43.77793 | B |
| 14 | 76.90419 | 41.17419 | B |
| 15 | 125.65833 | 48.87833 | B |
| 16 | 123.28171 | 44.50171 | B |
| 17 | 67.76310 | 39.18310 | B |
| 18 | 77.89094 | 42.16094 | B |
| 19 | 118.51827 | 41.73827 | B |
| 20 | 122.90330 | 44.12330 | B |
| 21 | 125.22900 | 85.37900 | C |
| 22 | 131.77034 | 84.77034 | C |
| 23 | 175.92367 | 87.87367 | C |
| 24 | 172.93231 | 82.88231 | C |
| 25 | 131.41047 | 91.56047 | C |
| 26 | 132.90734 | 85.90734 | C |
| 27 | 177.78237 | 89.73237 | C |
| 28 | 172.43964 | 82.38964 | C |
| 29 | 129.83182 | 89.98182 | C |
| 30 | 136.34132 | 89.34132 | C |
| 31 | 180.09259 | 90.46259 | D |
| 32 | 180.11401 | 88.48401 | D |
| 33 | 132.30074 | 90.87074 | D |
| 34 | 133.79616 | 85.21616 | D |
| 35 | 182.63329 | 93.00329 | D |
| 36 | 185.19807 | 93.56807 | D |
| 37 | 132.82043 | 91.39043 | D |
| 38 | 134.20258 | 85.62258 | D |
| 39 | 177.41525 | 87.78525 | D |
| 40 | 180.49311 | 88.86311 | D |
The data set anovaData has a column named CAMCOG_post which corresponds to the CAMCOG score after receiving the intervantion, the column CAMCOG_pre is the score before the intervention, and finally Group is a column representing the intervention group:
Condition A: Participants with mild cognitive impairment received the intervention.
Condition B: Participants with mild cognitive impairment did not receive the intervention.
Condition C: Healthy participants without cognitive impairment received the treatment.
Condition D: Healthy participants without cognitive impairment did not receive the treatment.
However, we will deal with this variable later in this practice.
RThe repeated measures t-test can be estimated by using the t-test() function like this:
Paired t-test
data: Pair(CAMCOG_post, CAMCOG_pre)
t = 17.59, df = 39, p-value < 2.2e-16
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
57.41718 72.33782
sample estimates:
mean difference
64.8775 How do we interpret the output? Similar to a test between groups, we will have a t value and degrees of freedom df, these values are relevant to find the \(p-value\). In the output we can observe that the p-value is a small number less than \(0.05\). Hence, the mean difference is not explained chance.
We can obtain the same result by estimating, you know what model …?
The \(t-test\) for non-independent samples is an acceptable model if you believe that the mean difference is really explained by only on factor: Time. You are assuming your intervantion caused a change overtime. In a real application, we need to add more variables to our list of predictors in order to adjust the results by multiple possible explanations. One option we have is to estiimate a regression model where you have more freedom to add multiple predictors.
Let’s compare the results after estimating the same model using a regression model:
Parameter | Coefficient | SE | 95% CI | t(38) | p
-------------------------------------------------------------------
(Intercept) | 58.21 | 10.50 | [36.96, 79.46] | 5.55 | < .001
CAMCOG pre | 1.10 | 0.15 | [ 0.79, 1.41] | 7.23 | < .001
Uncertainty intervals (equal-tailed) and p-values (two-tailed) computed
using a Wald t-distribution approximation.If you check carefully, I’m adding the score before the intervantion as a predictor of the score after the intervention. I’m doing it to get an estimate of the rate of change overtime. The model estimates showed that for 1-unit increment in the score before the intervantion, the post-treatment score increased 1.10 units. This rate of change is not explained by chance because the \(p\)-value is less than \(0.05\). This is a great model, it is telling me that overtime the score gets better. In simple words, it is indicating that aging adults got better overtime.
You may be thinking now, “wait… you told us that the intercept should be the mean of \(Y\)”. Yes, I said this in class, but remember that you will get the estimated mean of \(Y\) in a regression model when your observed predictors (independent variables) have zeros or comprises a range of values where zero makes sense. In this case, it does not make sense to have a score of zero in the CAMCOG test, a participant will always get at least 1 point. But, you could transform your independent variable into \(z\)-scores, in this case we can transform CAMCOG_pre into a \(z\) distributed variable. See how I use the function scale() to transform the values:
Parameter | Coefficient | SE | 95% CI | t(38) | p
--------------------------------------------------------------------
(Intercept) | 129.18 | 3.71 | [121.66, 136.70] | 34.78 | < .001
CAMCOG pre | 27.19 | 3.76 | [ 19.57, 34.80] | 7.23 | < .001
Uncertainty intervals (equal-tailed) and p-values (two-tailed) computed
using a Wald t-distribution approximation.CAMCOG_post and the intercept are really the same value. Use R to check it out. (5 points)Great! If you see the output now the intercept is the mean of \(Y\) when the predictor is \(0\). This happens when we include zero in the range of possible values in your predictor. In this case, we centered the variable CAMCOG_pre at zero, in simple words the mean is centered to zero.
| Variable | N = 401 |
|---|---|
| CAMCOG_pre | 64.30 (24.63) |
| CAMCOG_pre_Zscore | 0.00 (1.00) |
| 1 Mean (SD) | |
CAMCOG_pre into \(z\)-scores, are we changing the shape of the observed distribution? Create histograms to compare both variables. (5 points)Up to this point, I have explained you how you can analyze the difference of two repeated measures using regression. Nonetheless, I haven’t showed you why a Classical Regression Model is better than a paired \(t\)-test. To achieve this, it’s important to remind you that the intervention we are analyzing involves four distinct groups. So far, we have not included the variable representing group membership in the analysis, this is your next step in the following question:
Group as a new predictor. Interpret the results (10 points).We haven’t had time during this semester to practice moderation analysis. In the following questions you will work in R to conduct several steps important to test a moderated effect. It is likely that JAMOVI has a module on how to analyze this type of model but let’s focus on the code that we already have in the slides.
Estimate a Classical Regression Model where WAISR_block is the outcome or dependent variable, the predictors or independent variables are VO2peak, and Stroop_color. Interpret the results. (15 points)
You will need the next lines of code to open the data in R:
The next question will ask you to create a figure, you may use Word or Google Docs to create the figure or you could use the free online software app.diagrams.net.
VO2peak could be a moderator in the relation between WAISR_block and Stroop_color. Check slide 5 by clicking here and then create a conceptual model for this model. Add the figure to your answer. (5 points)Now you have a graphical representation of what you need to model, but this figure is not your analytical model.
Finally, I need to evaluate that I have tortured you enough! Complete the next question:
\(WAISRblock \sim \beta_{0} + \beta_{1}VO2peak_{1} + \beta_{2}StroopColor_{2} + ? + e\)
Up to this point we haven’t estimated a model where we test a possible moderation effect. Let’s do it now:
VO2peak is the moderator in the relationship of WAISR_block and Stroop_color. You may answer this question using R or Jamovi. If you estimate the model using Jamovi you should add the table showing the estimated values. Interepret the results. Is the interaction term explained by chance? How do you know? (20 points)At this point, you already estimated the moderation model, but you will need to estimate the simple slopes. Let’s continue:
interactions and the function sim_slopes. You could conduct the same analysis in JAMOVI but you will need extra steps explained here. Interpret the results. Are simple slopes at the three different levels of VO2peak explained by chance? (20 points)Finally, we need to create a plot to understand better the simple slopes.
marginaleffects.---
title: "Final Exam Fall 2024"
subtitle: "240 points"
title-block-banner: true
author: "Esteban Montenegro-Montenegro"
date: now
format:
live-html:
highlight-style: gruvbox
code-fold: true
code-tools: true
engine: knitr
webr:
packages:
- dplyr
- ggplot2
- parameters
theme:
light: sandstone
dark: cyborg
toc: true
toc-depth: 4
toc-title: Sections
self-contained: false
bibliography: references.bib
csl: apa.csl
editor:
markdown:
wrap: 72
code-annotations: hover
lightbox: true
---
{{< include ./_extensions/r-wasm/live/_knitr.qmd >}}
# Introduction
::: column-margin
{fig-alt="Keanu Reeves buried alive. It is a scene from a movie." width="200"}
:::
In this "exam" you will need to answer several theoretical questions, plus
`R` activities. Some of the hands on questions can be answered in `Jamovi` but, it will
take you more time to answer them using `Jamovi`. As always, this is just another
excuse for adding another lecture, my goal is that you are exposed to new topics
and statiscal models that are useful in psychology. You may work in pairs
this time and submit one single file for each team.
# Refresh theoretical concepts
1. A true experiment selects participants randomly, and assign
participants randomly to different conditions (10 points):
```{=html}
<input type="radio" id="html" name="is_yes" value="YES">
<label for="YES">Yes</label><br>
<input type="radio" id="html" name="is_no" value="NO">
<label for="NO">No</label><br>
```
------------------------------------------------------------------------
2. Qualitative research collects numerical values to reject the null
hypothesis (10 points):
```{=html}
<input type="radio" id="html" name="is_yes" value="YES">
<label for="YES">Yes</label><br>
<input type="radio" id="html" name="is_no" value="NO">
<label for="NO">No</label><br>
```
----------------------------------------------------------------------------
3. Mario needs to know if there is a causal relationship between sugar
intake and high BMI (Body Mass Index). What type of design should
Mario conduct? (10 points)
```{=html}
<input type="radio" id="html" name="op1" value="op1">
<label for="op1">Interview</label><br>
<input type="radio" id="html" name="op2" value="op2">
<label for="op2">Experiment</label><br>
<input type="radio" id="html" name="op3" value="op3">
<label for="op3">Qualitative design</label><br>
<input type="radio" id="html" name="op4" value="op4">
<label for="op4">All the above are true</label><br>
```
------------------------------------------------------------------------------
4. Select the option that will help you to collect counterfactual
evidence in an experiment: (10 points)
```{=html}
<input type="radio" id="html" name="op1" value="op1">
<label for="op1">Control group</label><br>
<input type="radio" id="html" name="op2" value="op2">
<label for="op2">Waiting list</label><br>
<input type="radio" id="html" name="op3" value="op3">
<label for="op3">Recruit participants online</label><br>
<input type="radio" id="html" name="op4" value="op4">
<label for="op4">Options 1 and 2 are correct</label><br>
```
------------------------------------------------------------------------------
5. If you estimate a correlation between two variables, you can also
assume causation: (10 points)
```{=html}
<input type="radio" id="html" name="is_yes" value="YES">
<label for="true">TRUE</label><br>
<input type="radio" id="html" name="is_no" value="NO">
<label for="false">FALSE</label><br>
```
-------------------------------------------------------------------------------
6. Write the three requirements of a causal relationship. (`HINT: Check Lecture 1`) (10 points)
-------------------------------------------------------------------------------
7. In the lecture titled: "Introduction to probability and statistics",
I showed the picture below. What is the meaning of this picture
following slide 3 ? (10 points)
------------------------------------------------------------------------------
8. Select only the TRUE statement: (10 points)
```{=html}
<input type="radio" id="html" name="op1" value="op1">
<label for="op1">Models are perfect representations of Nature</label><br>
<input type="radio" id="html" name="op2" value="op2">
<label for="op2">Data produces models</label><br>
<input type="radio" id="html" name="op3" value="op3">
<label for="op3">Models produce data, data does not produce models</label><br>
<input type="radio" id="html" name="op4" value="op4">
<label for="op4">All statistical models are perfectly correct</label><br>
```
-------------------------------------------------------------------------------
9. Parameters in a statistical model are unknown information, we
collect data to reduce the uncertainty in the parameters: (10 points)
```{=html}
<input type="radio" id="html" name="is_yes" value="YES">
<label for="true">TRUE</label><br>
<input type="radio" id="html" name="is_no" value="NO">
<label for="false">FALSE</label><br>
```
-------------------------------------------------------------------------------
10. The reduction in uncertainty about model parameters that you achieve
when you collect data is called statistical inference: (10 points)
```{=html}
<input type="radio" id="html" name="is_yes" value="YES">
<label for="true">TRUE</label><br>
<input type="radio" id="html" name="is_no" value="NO">
<label for="false">FALSE</label><br>
```
------------------------------------------------------------------------------
11. In the following correlation matrix, is the correlation ($r$ =
-0.053) between attention and rumZ explained by chance alone? (10 points)
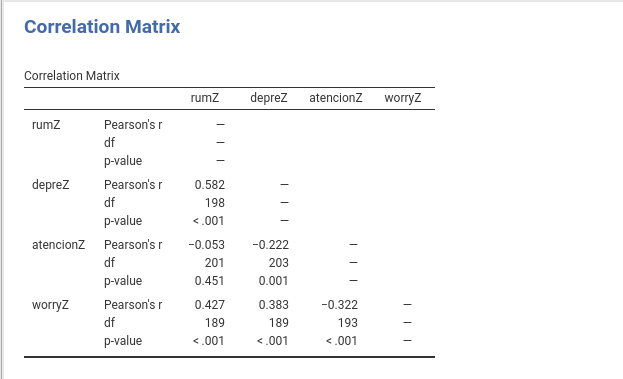
```{=html}
<input type="radio" id="html" name="is_yes" value="YES">
<label for="YES">Yes</label><br>
<input type="radio" id="html" name="is_no" value="NO">
<label for="NO">No</label><br>
```
------------------------------------------------------------------------------
# Repeated measures overtime
In my extra fun lectures, I got so excited teaching and I forgot
to talk more about repeated measures, and how can we analyze
*longitudinal data*. In the examples that I'll provide
we'll analyze only two measurements points. There are
other models to deal with multiple measures such as
your heart rate measured every second by your smart watch, or
the changes in working memory by month in toddlers; I
will not cover details about these models, but I'll try
to introduce some basics.
I will start from the simpliest case, the famous $t$-test
for repeated measures.
## To be *t-test* or not to be ...
Consider research designs where you evaluate your participants
before an intervention, and then you evaluate them again
after the intervention.
For example, you could develop an intervantion to help
your participants to stop smoking tobacco. You could
measure how many cigarettes they smoked before then intervention, and
asked again how many cigarettes are they consuming per day
after the intervention.
You may remember the data set `anovaData`. This data set
was the product of an intervention to reduce the dementia
symptons in a group of older adults in Costa Rica. You
may remember that the outcome variable is
the score in the total score in the CAMCOG test. The first
time we analyze this data we only tested
a one-way ANOVA on the post test. I didn't mention we
measured the cognitive performance before the intervention.
In this case we can ask the following question:
::: {.callout-tip}
## Research question
Are the CAMCOG scores before the intervantion different from
the CAMCOG scores after the intervantion?
:::
We can try to answer this question estimating a repeated
measures t-test.
First let's take a look at the data so you can remember the
variables in the data set.
```{r}
## Link to the data set:
dataLink <-"https://raw.githubusercontent.com/blackhill86/mm2/refs/heads/main/dataSets/anovaData.csv"
autoMemory <- read.csv(dataLink)
```
```{r}
library(kableExtra)
kbl(autoMemory) |>
kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive")) |>
scroll_box(width = "100%", height = "200px")
```
The data set `anovaData` has a column named `CAMCOG_post` which
corresponds to the CAMCOG score after receiving the intervantion, the
column `CAMCOG_pre` is the score before the intervention, and finally
`Group` is a column representing the intervention group:
- ***Condition A***: Participants with mild cognitive impairment
received the intervention.
- ***Condition B***: Participants with mild cognitive impairment
***did not*** receive the intervention.
- ***Condition C***: Healthy participants without cognitive impairment
received the treatment.
- ***Condition D***: Healthy participants without cognitive impairment
***did not*** receive the treatment.
However, we will deal with this variable later in this practice.
## Estimation in `R`
The repeated measures t-test can be estimated by using
the `t-test()` function like this:
```{r}
t.test(Pair(CAMCOG_post,CAMCOG_pre)~ 1,
data = autoMemory)
```
How do we interpret the output? Similar to a test between groups,
we will have a `t` value and degrees of freedom `df`, these
values are relevant to find the $p-value$. In the output
we can observe that the p-value is a small number
less than $0.05$. Hence, the mean difference is not
explained chance.
We can obtain the same result by estimating, you know what model ...?
### Estimating a Classical Regression Model with two measurement times
The $t-test$ for non-independent samples is an acceptable model if
you believe that the mean difference is really explained by only
on factor: *Time*. You are assuming your intervantion caused a change
overtime. In a real application, we need to add more variables
to our list of predictors in order to adjust the results by
multiple possible explanations. One option we have is to
estiimate a regression model where you have more
freedom to add multiple predictors.
Let's compare the results after estimating the same
model using a regression model:
```{r}
library(parameters)
mod <- lm(CAMCOG_post ~ CAMCOG_pre, data = autoMemory)
model_parameters(mod )
```
If you check carefully, I'm adding the score before the intervantion as a
predictor of the score after the intervention. I'm doing it to get
an estimate of the rate of change overtime. The model estimates showed
that for 1-unit increment in the score before the intervantion, the post-treatment
score increased 1.10 units. This rate of change is not explained by chance
because the $p$-value is less than $0.05$. This is a great model, it is telling
me that overtime the score gets better. In simple words, it is indicating
that aging adults got better overtime.
You may be thinking now, "wait... you told us that the intercept should be
the mean of $Y$". Yes, I said this in class, but remember that you will
get the estimated mean of $Y$ in a regression model when your observed
predictors (independent variables) have zeros or comprises a range of values where zero makes sense.
In this case, it does not make sense to have a score of zero in the CAMCOG
test, a participant will always get at least 1 point. But, you could
transform your independent variable into $z$-scores, in this case
we can transform `CAMCOG_pre` into a $z$ distributed variable. See
how I use the function `scale()` to transform the values:
```{r}
modZ <- lm(CAMCOG_post ~ scale(CAMCOG_pre), data = autoMemory)
model_parameters(modZ)
```
::: {.callout-important}
### Question 1
1. Check if the mean of `CAMCOG_post` and the intercept
are really the same value. Use `R` to check it out. (5 points)
:::
Great! If you see the output now the intercept is the mean of $Y$ when
the predictor is $0$. This happens when we include zero in the range
of possible values in your predictor. In this case, we centered the
variable `CAMCOG_pre` at zero, in simple words the mean is centered
to zero.
```{r}
#| warning: false
#| message: false
library(tidyverse)
autoMemory <- autoMemory |>
mutate(CAMCOG_pre_Zscore = as.numeric(scale(CAMCOG_pre)))
```
```{r}
#| echo: false
library(gtsummary)
autoMemory |>
tbl_summary(
include = c(CAMCOG_pre, CAMCOG_pre_Zscore),
statistic = list(
all_continuous() ~ "{mean} ({sd})",
all_categorical() ~ "{n} / {N} ({p}%)"
),
digits = all_continuous() ~ 2
) |>
modify_header(label ~ "**Variable**")|>
modify_caption("**Mean and Standard deviation of CAMCOG_pre**") |>
bold_labels()
```
::: {.callout-important}
### Question 2
2. After transforming `CAMCOG_pre` into $z$-scores,
are we changing the shape of the observed distribution?
Create histograms to compare both variables. (5 points)
:::
Up to this point, I have explained you how you can analyze the difference
of two repeated measures using regression. Nonetheless, I haven't showed you
why a Classical Regression Model is better than a paired $t$-test. To achieve this,
it’s important to remind you that the intervention we are analyzing involves four distinct groups. So far, we have not included the variable representing group membership in the analysis, this is your next step in the following question:
::: {.callout-important}
### Question 3
3. Modify the following code, add the variable `Group` as a new predictor.
Interpret the results (10 points).
```{webr}
#| include: false
dataLink <-"https://raw.githubusercontent.com/blackhill86/mm2/refs/heads/main/dataSets/anovaData.csv"
autoMemory <- read.csv(dataLink)
```
```{webr}
mod <- lm(CAMCOG_post ~ CAMCOG_pre, data = autoMemory)
model_parameters(mod)
```
:::
# Wild moderation in action
::: column-margin
{fig-alt="Bob Sponge meme where two fishes who are Police Officers show to Patrick
the next text: Fun headings my instructor creates to male laugh. In the frame below Patrick is
scared of the text" width="200"}
:::
We haven't had time during this semester to practice moderation analysis. In the
following questions you will work in `R` to conduct several steps
important to test a moderated effect. It is likely that `JAMOVI` has a module
on how to analyze this type of model but let's focus on the code that we already have
in the slides.
::: {.callout-important}
### Question 4
4. Estimate a Classical Regression Model where `WAISR_block` is the outcome or
dependent variable, the predictors or independent variables are `VO2peak`, and
`Stroop_color`. Interpret the results. (15 points)
You will need the next lines of code to open the data in `R`:
```{r}
url <- "https://raw.githubusercontent.com/blackhill86/mm2/refs/heads/main/dataSets/ouesData.csv"
ouesData <- read.csv(url)
```
:::
The next question will ask you to create a figure, you may use Word or Google Docs
to create the figure or you could use the free online software [app.diagrams.net.](https://app.diagrams.net/){target="_blank"}
::: {.callout-important}
### Question 5
5. It is possible that `VO2peak` could be a moderator
in the relation between `WAISR_block` and `Stroop_color`.
Check slide 5 by [clicking here](https://m-square.net/lecture11/moderation_polynomials.html#/how-do-you-interpret-an-interaction-effect){target="_blank"}
and then create a conceptual model for this model. Add the figure to your answer. (5 points)
:::
Now you have a graphical representation of what you need to model, but this figure is not
your *analytical model*.
::: {.callout-important}
### Question 7
6. Check Figure 2 in slide 5, you may [click here.](https://m-square.net/lecture11/moderation_polynomials.html#/the-world-can-show-you-interactions){target="_blank"}
After studying this figure, create an analytical figure corresponding to the previous model. (10 points)
:::
Finally, I need to evaluate that I have tortured you enough! Complete the next question:
::: {.callout-important}
### Question 8
7. Complete the following model representation, add the term that
is missing to estimate a moderation model (10 points):
$WAISRblock \sim \beta_{0} + \beta_{1}VO2peak_{1} + \beta_{2}StroopColor_{2} + ? + e$
:::
Up to this point we haven't estimated a model where we test
a possible moderation effect. Let's do it now:
::: {.callout-important}
### Question 9
8. Estimate a moderation model, in this model
`VO2peak` is the moderator in the relationship
of `WAISR_block` and `Stroop_color`. You may answer
this question using `R` or `Jamovi`. If you
estimate the model using `Jamovi` you should
add the table showing the estimated values.
Interepret the results. Is the interaction term
explained by chance? How do you know? (20 points)
:::
At this point, you already estimated the moderation model,
but you will need to estimate the simple slopes. Let's continue:
::: {.callout-important}
### Question 10
9. Pay attention to slide 14 ([CLICK HERE](https://m-square.net/lecture11/moderation_polynomials.html#/simple-slopes-johnson-neyman-technique-in-r){target="_blank"}), then estimate the simple slopes using the package
`interactions` and the function `sim_slopes`. You could conduct the same
analysis in `JAMOVI` but you will need extra steps explained [here.](https://m-square.net/lecture11/moderation_polynomials.html#/simple-slopes-estimation-centering-1){target="_blank"}
Interpret the results. Are simple slopes at the three different levels of
`VO2peak` explained by chance? (20 points)
:::
Finally, we need to create a plot to understand better
the simple slopes.
::: {.callout-important}
### Question 11
10. Check the code I wrote to
create the figure in slide 6 ([CLICK HERE](https://m-square.net/lecture11/moderation_polynomials.html#/how-do-you-interpret-an-interaction-effect-1){target="_blank"}). Copy the same code an replace the code as necessary. (20 points)
Remember, you will need to install the package `marginaleffects`.
:::